
【题目】已知向量 ![]() =(
=( ![]() sin3x,﹣y),
sin3x,﹣y), ![]() =(m,cos3x﹣m)(m∈R),且
=(m,cos3x﹣m)(m∈R),且 ![]() +
+ ![]() =
= ![]() .设y=f(x).
.设y=f(x).
(1)求f(x)的表达式,并求函数f(x)在[ ![]() ,
, ![]() ]上图象最低点M的坐标.
]上图象最低点M的坐标.
(2)在△ABC中,f(A)=﹣ ![]() ,且A>
,且A> ![]() π,D为边BC上一点,AC=
π,D为边BC上一点,AC= ![]() DC,BD=2DC,且AD=2
DC,BD=2DC,且AD=2 ![]() ,求线段DC的长.
,求线段DC的长.
【答案】
(1)解:向量 ![]() =(
=( ![]() sin3x,﹣y),
sin3x,﹣y), ![]() =(m,cos3x﹣m)(m∈R),
=(m,cos3x﹣m)(m∈R),
∴ ![]() +
+ ![]() =(m+
=(m+ ![]() sin3x,﹣y+cos3x﹣m),
sin3x,﹣y+cos3x﹣m),
∵ ![]() +
+ ![]() =
= ![]() .
.
m+ ![]() sin3x=0,﹣y+cos3x﹣m=0
sin3x=0,﹣y+cos3x﹣m=0
∴y=cos3x+ ![]() sin3x
sin3x
即y=f(x)=2sin(3x+ ![]() )
)
∴f(x)的表达式f(x)=2sin(3x+ ![]() )
)
∵x在[ ![]() ,
, ![]() ]上,
]上,
∴3x+ ![]() ∈[
∈[ ![]() ,
, ![]() ],
],
当3x+ ![]() =
= ![]() 时,取得最低点,此时x=
时,取得最低点,此时x= ![]() ,y=﹣1.
,y=﹣1.
∴函数f(x)在[ ![]() ,
, ![]() ]上图象最低点M的坐标为(
]上图象最低点M的坐标为( ![]() ,﹣1).
,﹣1).
(2)解:由f(A)=﹣ ![]() ,即2sin(3A+
,即2sin(3A+ ![]() )=
)= ![]()
可得:3A+ ![]() =
= ![]() +2kπ或3A+
+2kπ或3A+ ![]() =
= ![]() +2kπ,k∈Z.
+2kπ,k∈Z.
∵π>A> ![]() π,
π,
∴A= ![]() .
.
∴△ABC是直角三角形.
AC= ![]() DC,BD=2DC,
DC,BD=2DC,
设DC=x,则AC= ![]() x,BD=2x,BC=3x.
x,BD=2x,BC=3x.
可得:AB= ![]() .
.
在三角形ADB和三角形ADC中,由余弦定理:可得cos∠BDA= ![]()
cos∠ADC= ![]() ,
,
∵∠ADC+∠BDA=π.
∴ ![]() =﹣
=﹣ ![]() ,
,
解得:x= ![]() .
.
∴线段DC的长为 ![]() .
.
【解析】(1)根据 ![]() +
+ ![]() =
= ![]() .用x表示y可得f(x)的表达式.即可求函数f(x)在[
.用x表示y可得f(x)的表达式.即可求函数f(x)在[ ![]() ,
, ![]() ]上图象最低点M的坐标.(2)根据f(A)=﹣
]上图象最低点M的坐标.(2)根据f(A)=﹣ ![]() ,且A>
,且A> ![]() π,求出A,AC=
π,求出A,AC= ![]() DC,BD=2DC,且AD=2
DC,BD=2DC,且AD=2 ![]() ,利用余弦定理求出线段DC的长.
,利用余弦定理求出线段DC的长.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD .

(1)求证:CD⊥平面ABD;
(2)若AB=BD=CD=1,M为AD中点,求三棱锥A-MBC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.命题“若x2=9,则x=±3”的否命题为“若x2=9,则x≠±3”
B.若命题P:?x0∈R, ![]() ,则命题?P:?x∈R,
,则命题?P:?x∈R, ![]()
C.设 ![]() 是两个非零向量,则“
是两个非零向量,则“ ![]() 是“
是“ ![]() 夹角为钝角”的必要不充分条件
夹角为钝角”的必要不充分条件
D.若命题P: ![]() ,则¬P:
,则¬P: ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°. 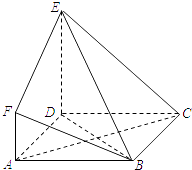
(1)求证:AC⊥平面BDE;
(2)设点M是线段BD上一个动点,试确定点M的位置,使得AM∥平面BEF,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点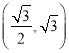 ,离心率为
,离心率为![]() .
.
(1)求椭圆的标准方程;
(2)过椭圆的上顶点作直线![]() 交抛物线
交抛物线![]() 于
于![]() 两点,
两点, ![]() 为原点.
为原点.
①求证: ![]() ;
;
②设![]() 、
、![]() 分别与椭圆相交于
分别与椭圆相交于![]() 、
、![]() 两点,过原点
两点,过原点![]() 作直线
作直线![]() 的垂线
的垂线![]() ,垂足为
,垂足为![]() ,证明:
,证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx+1(a,b为实数),设![]() ,
,
(1)若f(-1)=0,且对任意实数x均有f(x)≥0成立,求F(x)的表达式;
(2)在(1)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围;
(3)设mn<0,m+n>0,a>0,且f(x)满足f(-x)=f(x),试比较F(m)+F(n)的值与0的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AB∥C,AD=DC=CB=1,∠ABC═60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1. 
(1)求证:BC⊥平面ACFE;
(2)求二面角A﹣BF﹣C的平面角的余弦值;
(3)若点M在线段EF上运动,设平MAB与平FCB所成二面角的平面角为θ(θ≤90°),试求cosθ的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com