
【题目】已知函数f(x)是定义在R上的奇函数,并且当x∈(0,+∞)时,f(x)=2x.
(1)求f(log2![]() )的值;
)的值;
(2)求f(x)的解析式.
【答案】(1)-3. (2) f(x)=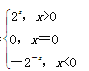 .
.
【解析】
试题(1)因为f(x)为奇函数,且当x∈(0,+∞)时,f(x)=2x,
所以f(log2![]() )=f(-log23)=-f(log23)=-2log23=-3. (6分)
)=f(-log23)=-f(log23)=-2log23=-3. (6分)
(2)设任意的x∈(-∞,0),则-x∈(0,+∞),
因为当x∈(0,+∞)时,f(x)=2x,所以f(-x)=2-x,
又因为f(x)是定义在R上的奇函数,则f(-x)=-f(x),
所以f(x)=-f(-x)=-2-x,即当x∈(-∞,0)时,f(x)=-2-x; (8分)
又因为f(0)=-f(0),所以f(0)=0, (10分)
综上可知,f(x)=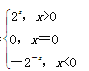 . (12分)
. (12分)


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】“秃发”是一种常见的毛发疾病,随着发病人群年龄结构的年变化,逐渐引起了社会的广泛关注.一个人出生时头发数量约为100000根,数学徐老师建立了“秃发”函数模型作预估:一个人![]() 岁时的头发根数为
岁时的头发根数为![]() ,其中
,其中![]() 称为“脱发指数”.
称为“脱发指数”.
(1)杜老师5岁时有74375根头发,请依据模型求出杜老师的“脱发指数”![]() 的值;
的值;
(2)徐老师的学生认为“秃发”函数模型中有两个缺点:①头发的根数应该为整数;②头发的根数不能为负数,徐老师感觉很有道理,将模型作了两处修正,请写出修正后(1)问中杜老师的“秃发”函数模型,并求出杜老师几岁时头发最多.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列四个命题:
①函数![]() 满足:对任意
满足:对任意![]() 有
有![]() ;
;
②函数![]() 均为奇函数;
均为奇函数;
③若函数![]() 在
在![]() 上有意义,则
上有意义,则![]() 的取值范围是
的取值范围是![]() ;
;
④设![]() 是关于
是关于![]() 的方程
的方程![]() ,(
,(![]() 且
且![]() )的两根,则
)的两根,则![]() ;
;
其中正确命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为偶函数.
为偶函数.
(1)求实数![]() 的值,并写出
的值,并写出![]() 在区间
在区间![]() 上的增减性和值域(不需要证明);
上的增减性和值域(不需要证明);
(2)令![]() ,其中
,其中![]() ,若
,若![]() 对任意
对任意![]() 、
、![]() ,总有
,总有![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)令![]() ,若
,若![]() 对任意
对任意![]() 、
、![]() ,总有
,总有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】口袋里装有1红,2白,3黄共6个形状相同的小球,从中取出2球,事件![]() “取出的两球同色”,
“取出的两球同色”,![]() “取出的2球中至少有一个黄球”,
“取出的2球中至少有一个黄球”,![]() “取出的2球至少有一个白球”,
“取出的2球至少有一个白球”,![]() “取出的两球不同色”,
“取出的两球不同色”,![]() “取出的2球中至多有一个白球”.下列判断中正确的序号为________.
“取出的2球中至多有一个白球”.下列判断中正确的序号为________.
①![]() 与
与![]() 为对立事件;②
为对立事件;②![]() 与
与![]() 是互斥事件;③
是互斥事件;③![]() 与
与![]() 是对立事件:④
是对立事件:④![]() ;⑤
;⑤![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面A1B1C1,AA1=1,底面三角形A1B1C1是边长为2的正三角形,E是BC中点,则下列说法正确的是( )

①CC1与AB1所成角的余弦值为![]()
②AB⊥平面ACC1A1
③三角形AB1E为直角三角形
④A1C1∥平面AB1E
A.①②B.③④C.①③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
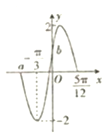
【题目】函数f(x)=Asin(2ωx+φ)(A>0,ω>0,|φ|<![]() )的部分图象如图所示
)的部分图象如图所示
(1)求A,ω,φ的值;
(2)求图中a,b的值及函数f(x)的递增区间;
(3)若α∈[0,π],且f(α)=![]() ,求α的值.
,求α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】哈师大附中高三学年统计甲、乙两个班级一模数学分数(满分150分),每个班级20名同学,现有甲、乙两位同学的20次成绩如下列茎叶图所示:

(I)根据基叶图求甲、乙两位同学成绩的中位数,并将乙同学的成绩的频率分布直方图填充完整;

(Ⅱ)根据基叶图比较甲乙两位同学数学成绩的平均值及稳定程度(不要求计算出具体值,给出结论即可)
(Ⅲ)现从甲乙两位同学的不低于140分的成绩中任意选出2个成绩,设事件![]() 为“其中2 个成绩分别属于不同的同学”,求事件
为“其中2 个成绩分别属于不同的同学”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com