
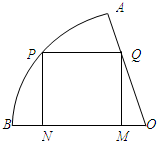
 如图,在半径为
如图,在半径为| 3 |
| π |
| 12 |
| 10 |
2
| ||
| 5 |
| 3 |
| 3 |
| QM |
| tan60° |
| 3 |
| 3 |
| 3 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 4 |
2
| ||
| 5 |
| 1-cos2B |
| asinB |
| sinA |
| asinC |
| sinA |
| 3 |
| 3 |
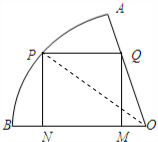
| QM |
| tan60° |
| PN | ||
|
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| π |
| 6 |
| ||
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 12 |
| π |
| 4 |
2
| ||
| 5 |
| 1-cos2B |
| ||
| 5 |
| a |
| sinA |
| b |
| sinB |
| asinB |
| sinA |
| ||||||
|
| ||
| 2 |
2
| ||
| 5 |
| ||
| 2 |
| ||
| 5 |
3
| ||
| 10 |
| a |
| sinA |
| c |
| sinC |
| asinC |
| sinA |
| ||||||
|
| 2 |
| 2 |
| 2 |
| π |
| 4 |
| 13 |


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:
| A、{x|-10≤x≤15} |
| B、{x|-10≤x<10} |
| C、{x|x≤15} |
| D、{x|x<10} |
查看答案和解析>>
科目:高中数学 来源: 题型:
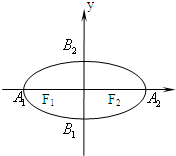 如图,椭圆的中心在坐标原点,焦点在x轴上,A1,A2,B1,B2椭圆顶点,F2为右焦点,延长B1F2与A2B2交于点P,若∠B1PA2为钝角,则该椭圆离心率的取值范围是( )
如图,椭圆的中心在坐标原点,焦点在x轴上,A1,A2,B1,B2椭圆顶点,F2为右焦点,延长B1F2与A2B2交于点P,若∠B1PA2为钝角,则该椭圆离心率的取值范围是( )A、(
| ||||
B、(0,
| ||||
C、(0,
| ||||
D、(
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 | 看电视 | 运动 | 总计 |
| 女性 | |||
| 男性 | |||
| 总计 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com