
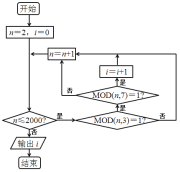
ΓΨΧβΡΩΓΩ1852ΡξΘ§”ΔΙζά¥ΜΣ¥ΪΫΧ ΩΈΑΝ“―«ΝΠΫΪΓΕΥοΉ”ΥψΨ≠ΓΖ÷–ΓΑΈο≤Μ÷Σ ΐΓ±Έ ΧβΒΡΫβΖ®¥Ϊ÷Ν≈Ζ÷ό.1874ΡξΘ§”ΔΙζ ΐ―ßΦ“¬μΈς…≠÷Η≥ω¥ΥΖ®ΖϊΚœ1801Ρξ”…ΗΏΥΙΒΟΒΫΒΡΙΊ”ΎΆ§”ύ ΫΫβΖ®ΒΡ“ΜΑψ–‘Ε®άμΘ§“ρΕχΈςΖΫ≥Τ÷°ΈΣΓΑ÷–Ιζ Θ”ύΕ®άμΓ±.ΓΑ÷–Ιζ Θ”ύΕ®άμΓ±Ϋ≤ΒΡ «“ΜΗωΙΊ”Ύ’ϊ≥ΐΒΡΈ ΧβΘ§άΐ»γ«σ1ΒΫ2000’β2000Ηω’ϊ ΐ÷–Θ§Ρή±Μ3≥ΐ”ύ1«“±Μ7≥ΐ”ύ1ΒΡ ΐΒΡΗω ΐΘ§œ÷”…≥Χ–ρΩρΆΦΘ§Τδ÷–MODΚ· ΐ «“ΜΗω«σ”ύΚ· ΐΘ§Φ«![]() ±μ Ψm≥ΐ“‘nΒΡ”ύ ΐΘ§άΐ»γ
±μ Ψm≥ΐ“‘nΒΡ”ύ ΐΘ§άΐ»γ![]() Θ§‘ρ δ≥ωiΈΣΘ® Θ©.
Θ§‘ρ δ≥ωiΈΣΘ® Θ©.
A.98B.97C.96D.95
 Κ°ΦΌ―ß”κΝΖœΒΝ–¥πΑΗ
Κ°ΦΌ―ß”κΝΖœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΝΥΒςΫΎΗΏ»ΐ―ß…ζ―ßœΑ―ΙΝΠΘ§Ρ≥–ΘΗΏ»ΐΡξΦΕΨΌ––ΝΥΑΈΚ”±»»ϋΘ§‘Ύ»ϋ«Α»ΐΈΜάœ ΠΕ‘«Α»ΐΟϊΫχ––ΝΥ‘Λ≤βΘ§”Ύ «”–ΝΥ“‘œ¬Ε‘ΜΑΘΚάœ ΠΦΉΘΚΓΑ7ΑύΡ–…ζ±»ΫœΉ≥Θ§7ΑύΩœΕ®ΒΟΒΎ“ΜΟϊΓ±Θ°άœ Π““ΘΚΓΑΈ“ΨθΒΟ14Αύ±»15Αύ«ΩΘ§14ΑύΟϊ¥ΈΜα±»15ΑύΩΩ«ΑΓ±Θ°άœ Π±ϊΘΚΓΑΈ“ΨθΒΟ7ΑύΡή”°15ΑύΓ±Θ°ΉνΚσάœ ΠΕΓ»ΞΙέΩ¥ΆξΝΥ±»»ϋΘ§ΜΊά¥ΚσΥΒΘΚΓΑ»Ζ Β «’β»ΐΗωΑύΒΟΝΥ«Α»ΐΟϊΘ§«“Έό≤ΔΝ–Θ§ΒΪ «ΡψΟ«»ΐ»Υ÷–÷Μ”–“Μ»Υ‘Λ≤βΉΦ»ΖΓ±Θ°Ρ«Ο¥Θ§ΜώΒΟ“ΜΓΔΕΰΓΔ»ΐΟϊΒΡΑύΦΕ“ά¥ΈΈΣ( )
A.7ΑύΓΔ14ΑύΓΔ15ΑύB.14ΑύΓΔ7ΑύΓΔ15Αύ
C.14ΑύΓΔ15ΑύΓΔ7ΑύD.15ΑύΓΔ14ΑύΓΔ7Αύ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΥΪ«ζœΏCΘΚ![]() 1Θ®a
1Θ®a![]() 0Θ§b
0Θ§b![]() 0Θ©ΒΡΉσ”“ΫΙΒψΖ÷±πΈΣF1Θ§F2Θ§ΒψOΈΣΉχ±ξ‘≠ΒψΘ§ΒψP‘ΎΥΪ«ζœΏΒΡ”“÷ß…œΘ§«“¬ζΉψ|F1F2|=2|OP|.»τ÷±œΏPF2”κΥΪ«ζœΏC÷Μ”–“ΜΗωΫΜΒψΘ§‘ρΥΪ«ζœΏCΒΡάκ–Ρ¬ ΈΣ( )
0Θ©ΒΡΉσ”“ΫΙΒψΖ÷±πΈΣF1Θ§F2Θ§ΒψOΈΣΉχ±ξ‘≠ΒψΘ§ΒψP‘ΎΥΪ«ζœΏΒΡ”“÷ß…œΘ§«“¬ζΉψ|F1F2|=2|OP|.»τ÷±œΏPF2”κΥΪ«ζœΏC÷Μ”–“ΜΗωΫΜΒψΘ§‘ρΥΪ«ζœΏCΒΡάκ–Ρ¬ ΈΣ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…ηΚ· ΐfΘ®xΘ©ΘΫex©¹ax+aΘ®aΓ RΘ©Θ§ΤδΆΦœσ”κx÷αΫΜ”ΎAΘ®x1Θ§0Θ©Θ§BΘ®x2Θ§0Θ©ΝΫΒψΘ§«“x1ΘΦx2Θ°
Θ®1Θ©«σaΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®2Θ©÷ΛΟςΘΚfΓδΘ®![]() Θ©ΘΦ0Θ®fΓδΘ®xΘ©ΈΣΚ· ΐfΘ®xΘ©ΒΡΒΦΚ· ΐΘ©ΘΜ
Θ©ΘΦ0Θ®fΓδΘ®xΘ©ΈΣΚ· ΐfΘ®xΘ©ΒΡΒΦΚ· ΐΘ©ΘΜ
Θ®3Θ©…ηΒψC‘ΎΚ· ΐyΘΫfΘ®xΘ©ΒΡΆΦœσ…œΘ§«“ΓςABCΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§Φ«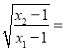 tΘ§«σΘ®a©¹1Θ©Θ®t©¹1Θ©ΒΡ÷ΒΘ°
tΘ§«σΘ®a©¹1Θ©Θ®t©¹1Θ©ΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§’ΐΥΡάβΉΕ![]() ΒΡΒΉΟφ±Ώ≥ΛΈΣ
ΒΡΒΉΟφ±Ώ≥ΛΈΣ![]() Θ§
Θ§![]() ΓΔ
ΓΔ![]() Ζ÷±πΈΣ
Ζ÷±πΈΣ![]() ΓΔ
ΓΔ![]() ΒΡ÷–Βψ.
ΒΡ÷–Βψ.
Θ®1Θ©Β±![]() ±Θ§÷ΛΟςΘΚΤΫΟφ
±Θ§÷ΛΟςΘΚΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®2Θ©»τΤΫΟφ![]() ”κΒΉΟφ
”κΒΉΟφ![]() Υυ≥…»ώΕΰΟφΫ«ΈΣ
Υυ≥…»ώΕΰΟφΫ«ΈΣ![]() Θ§«σ÷±œΏ
Θ§«σ÷±œΏ![]() ”κΤΫΟφ
”κΤΫΟφ![]() Υυ≥…Ϋ«ΒΡ’ΐœ“÷Β.
Υυ≥…Ϋ«ΒΡ’ΐœ“÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
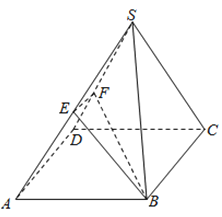
ΓΨΧβΡΩΓΩ“―÷ΣΆ÷‘≤![]() ΒΡάκ–Ρ¬ ΈΣ
ΒΡάκ–Ρ¬ ΈΣ![]() Θ§ΉσΓΔ”“ΫΙΒψΖ÷±π «
Θ§ΉσΓΔ”“ΫΙΒψΖ÷±π «![]() Θ§Ά÷‘≤
Θ§Ά÷‘≤![]() …œΕΧ÷αΒΡ“ΜΗωΕΥΒψ”κΝΫΗωΫΙΒψΙΙ≥…ΒΡ»ΐΫ«–ΈΒΡΟφΜΐΈΣ
…œΕΧ÷αΒΡ“ΜΗωΕΥΒψ”κΝΫΗωΫΙΒψΙΙ≥…ΒΡ»ΐΫ«–ΈΒΡΟφΜΐΈΣ![]() ΘΜ
ΘΜ
Θ®1Θ©«σΆ÷‘≤![]() ΒΡΖΫ≥ΧΘΜ
ΒΡΖΫ≥ΧΘΜ
Θ®2Θ©Ιΐ![]() Ής¥Ι÷±”Ύ
Ής¥Ι÷±”Ύ![]() ÷αΒΡ÷±œΏ
÷αΒΡ÷±œΏ![]() ΫΜΆ÷‘≤
ΫΜΆ÷‘≤![]() ”Ύ
”Ύ![]() ΝΫΒψΘ®Βψ
ΝΫΒψΘ®Βψ![]() ‘ΎΒΎΕΰœσœόΘ©Θ§
‘ΎΒΎΕΰœσœόΘ©Θ§![]() «Ά÷‘≤…œΈΜ”Ύ÷±œΏ
«Ά÷‘≤…œΈΜ”Ύ÷±œΏ![]() ΝΫ≤ύΒΡΕ·ΒψΘ§»τ
ΝΫ≤ύΒΡΕ·ΒψΘ§»τ![]() Θ§«σ÷ΛΘΚ÷±œΏ
Θ§«σ÷ΛΘΚ÷±œΏ![]() ΒΡ–±¬ ΈΣΕ®÷Β.
ΒΡ–±¬ ΈΣΕ®÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΥΡάβΉΕ![]() ÷–Θ§ΒΉΟφ
÷–Θ§ΒΉΟφ![]() ΈΣ÷±Ϋ«Χί–ΈΘ§
ΈΣ÷±Ϋ«Χί–ΈΘ§![]() ΓΈ
ΓΈ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§ΤΫΟφ
Θ§ΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() Θ§
Θ§![]() Θ§
Θ§![]() .
.

Θ®1Θ©«σ÷ΛΘΚ![]() ΘΜ
ΘΜ
Θ®2Θ©«σΕΰΟφΫ«![]() ΒΡ”ύœ“÷Β.
ΒΡ”ύœ“÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§“‘‘≠ΒψOΈΣΦΪΒψΘ§x÷αΒΡ’ΐΑκ÷αΈΣΦΪ÷αΫ®ΝΔΦΪΉχ±ξœΒΘ§ΝΫ÷÷Ήχ±ξœΒ÷–»ΓœύΆ§ΒΡ≥ΛΕ»ΒΞΈΜ.“―÷Σ÷±œΏlΒΡ≤Έ ΐΖΫ≥ΧΈΣ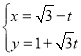 Θ®tΈΣ≤Έ ΐΘ©Θ§«ζœΏCΒΡΦΪΉχ±ξΖΫ≥ΧΈΣΠ―ΘΫ4sinΘ®Π»+
Θ®tΈΣ≤Έ ΐΘ©Θ§«ζœΏCΒΡΦΪΉχ±ξΖΫ≥ΧΈΣΠ―ΘΫ4sinΘ®Π»+![]() Θ©.
Θ©.
Θ®1Θ©«σ÷±œΏlΒΡΤ’Ά®ΖΫ≥Χ”κ«ζœΏCΒΡ÷±Ϋ«Ήχ±ξΖΫ≥ΧΘΜ
Θ®2Θ©»τ÷±œΏl”κ«ζœΏCΫΜ”ΎMΘ§NΝΫΒψΘ§«σΓςMONΒΡΟφΜΐ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ‘≤![]() Θ§Βψ
Θ§Βψ![]() Θ§
Θ§![]() «‘≤…œ“ΜΕ·ΒψΘ§Βψ
«‘≤…œ“ΜΕ·ΒψΘ§Βψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() …œΘ§Βψ
…œΘ§Βψ![]() ‘ΎΑκΨΕ
‘ΎΑκΨΕ![]() …œΘ§«“¬ζΉψ
…œΘ§«“¬ζΉψ![]() .
.
Θ®1Θ©Β±![]() ‘Ύ‘≤…œ‘ΥΕ· ±Θ§«σΒψ
‘Ύ‘≤…œ‘ΥΕ· ±Θ§«σΒψ![]() ΒΡΙλΦΘ
ΒΡΙλΦΘ![]() ΒΡΖΫ≥ΧΘΜ
ΒΡΖΫ≥ΧΘΜ
Θ®2Θ©…ηΙΐΒψ![]() ΒΡ÷±œΏ
ΒΡ÷±œΏ![]() ”κΙλΦΘ
”κΙλΦΘ![]() ΫΜ”ΎΒψ
ΫΜ”ΎΒψ![]() Θ®
Θ®![]() ≤Μ‘Ύ
≤Μ‘Ύ![]() ÷α…œΘ©Θ§¥Ι÷±”Ύ
÷α…œΘ©Θ§¥Ι÷±”Ύ![]() ΒΡ÷±œΏΫΜ
ΒΡ÷±œΏΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§”κ
Θ§”κ![]() ÷αΫΜ”ΎΒψ
÷αΫΜ”ΎΒψ![]() Θ§»τ
Θ§»τ![]() Θ§«σΒψ
Θ§«σΒψ![]() ΚαΉχ±ξΒΡ»Γ÷ΒΖΕΈß.
ΚαΉχ±ξΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com