
【题目】对于定义在区间D上的函数![]() :若存在闭区间
:若存在闭区间![]() 和常数e,使得对任意
和常数e,使得对任意![]() ,都有
,都有![]() ,且对任意
,且对任意![]() ,当
,当![]() 时,
时,![]() 恒成立,则称函数
恒成立,则称函数![]() 为区间D上的“平底型”函数.
为区间D上的“平底型”函数.
(1)判断函数![]() 和
和![]() 是否为R上的“平底型”函数?并说明理由;
是否为R上的“平底型”函数?并说明理由;
(2)若函数![]() 是区间
是区间![]() 上的“平底型”函数,求m和n的值.
上的“平底型”函数,求m和n的值.
【答案】(1)![]() 是平底型函数,
是平底型函数,![]() 不是平底型函数,理由见解析(2)
不是平底型函数,理由见解析(2)![]()
【解析】
(1)先分段讨论去绝对值符号,再求函数的值域,再结合“平底型”函数的性质判断即可得解;
(2)由函数![]() 为“平底型”函数等价于
为“平底型”函数等价于![]() ,则可解出
,则可解出![]() 的值,然后再将值代入运算即可得解.
的值,然后再将值代入运算即可得解.
解:(1)对于函数![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
故![]() 为“平底型”函数,
为“平底型”函数,
对于函数![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
即不存在闭区间![]() ,使当
,使当![]() 时,
时,![]() 恒成立,
恒成立,
故![]() 不为“平底型”函数;
不为“平底型”函数;
(2)由“平底型”函数定义可知,存在闭区间![]() 和常数e,使得对任意
和常数e,使得对任意![]() ,都有
,都有![]() ,
,
即![]() ,
,
所以![]() 恒成立,
恒成立,
即![]() 恒成立,
恒成立,
即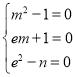 ,解得
,解得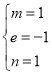 或
或 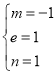 ,
,
①当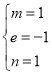 时,
时,![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
即函数![]() 为“平底型”函数,
为“平底型”函数,
②当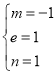 时,
时,![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
即函数![]() 不为“平底型”函数,
不为“平底型”函数,
综上可得:函数![]() 是区间
是区间![]() 上的“平底型”函数,则
上的“平底型”函数,则![]() .
.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
【题目】在中学生综合素质评价某个维度的测评中,分优秀、合格、尚待改进三个等级进行学生互评.某校高一年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了45名学生的测评结果,并作出频数统计表如下:
表一:男生
男生 | 等级 | 优秀 | 合格 | 尚待改进 |
频数 | 15 |
| 5 |
表二:女生
女生 | 等级 | 优秀 | 合格 | 尚待改进 |
频数 | 15 | 3 |
|
(1)求![]() ,
,![]() 的值;
的值;
(2)从表一、二中所有尚待改进的学生中随机抽取3人进行交谈,记其中抽取的女生人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望;
的分布列及数学期望;
(3)由表中统计数据填写![]() 列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
男生 | 女生 | 总计 | |
优秀 | |||
非优秀 | |||
总计 | 45 |
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
| 0.01 | 0.05 | 0.01 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知变量![]() 、
、![]() 之间的线性回归方程为
之间的线性回归方程为![]() ,且变量
,且变量![]() 、
、![]() 之间的一-组相关数据如下表所示,则下列说法错误的是( )
之间的一-组相关数据如下表所示,则下列说法错误的是( )
|
|
|
|
|
|
|
|
|
|
A.可以预测,当![]() 时,
时,![]() B.
B.![]()
C.变量![]()
![]() 之间呈负相关关系D.该回归直线必过点
之间呈负相关关系D.该回归直线必过点![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在时钟的表盘上作9个![]() 的扇形,每一个都覆盖4个数字,每两个覆盖的数字不全相同.求证:一定可以找到3个扇形,恰好覆盖整个表盘.举一个反例说明,作8个扇形将不具有上述性质.
的扇形,每一个都覆盖4个数字,每两个覆盖的数字不全相同.求证:一定可以找到3个扇形,恰好覆盖整个表盘.举一个反例说明,作8个扇形将不具有上述性质.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆周上有1994个点,将它们染成若干种不同的颜色,且每种颜色的点数各不相同.今在每种颜色的点集中各取一个点,组成顶点颜色各不相同的圆内接多边形,为了要使这样的多边形个数最多,应将1994个点染成多少种不同的颜色?且每种颜色的点集各含有多少个点?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线y=ax+1和抛物线y2=4x相交于不同的A,B两点.
(Ⅰ)若a=-2,求弦长|AB|;
(Ⅱ)若以AB为直径的圆经过原点O,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图像向右平移
的图像向右平移![]() 个单位后得到函数
个单位后得到函数![]() ,则
,则![]() 具有性质( )
具有性质( )
A.最大值为1,图像关于直线![]() 对称
对称
B.周期为![]() ,图像关于点
,图像关于点![]() 对称
对称
C.在![]() 上单调递增,为偶函数
上单调递增,为偶函数
D.在![]() 上单调递减,为奇函数
上单调递减,为奇函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某校九年级400名学生的体质情况,随机抽查了20名学生,测试1 min仰卧起坐的成绩(次数),测试成绩如下:
30 35 32 33 28 36 34 28 25 40
28 32 30 42 37 36 33 31 26 24
(1)20名学生的平均成绩![]() 是多少?标准差
是多少?标准差![]() 是多少?
是多少?
(2)次数位于![]() 与
与![]() 之间有多位同学?所占的百分比是多少?
之间有多位同学?所占的百分比是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ,若g(x)=f(x)-a恰好有3个零点,则a的取值范围为( )
,若g(x)=f(x)-a恰好有3个零点,则a的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
![]() 恰好有3个零点, 等价于
恰好有3个零点, 等价于![]() 的图象有三个不同的交点,
的图象有三个不同的交点,
作出![]() 的图象,根据数形结合可得结果.
的图象,根据数形结合可得结果.

![]() 恰好有3个零点,
恰好有3个零点,
等价于![]() 有三个根,
有三个根,
等价于![]() 的图象有三个不同的交点,
的图象有三个不同的交点,
作出![]() 的图象,如图,
的图象,如图,
由图可知,
当![]() 时,
时,![]() 的图象有三个交点,
的图象有三个交点,
即当![]() 时,
时,![]() 恰好有3个零点,
恰好有3个零点,
所以,![]() 的取值范围是
的取值范围是![]() ,故选D.
,故选D.
【点睛】
本题主要考查函数的零点与分段函数的性质,属于难题. 函数的性质问题以及函数零点问题是高考的高频考点,考生需要对初高中阶段学习的十几种初等函数的单调性、奇偶性、周期性以及对称性非常熟悉;另外,函数零点的几种等价形式:函数![]() 的零点
的零点![]() 函数
函数![]() 在
在![]() 轴的交点
轴的交点![]() 方程
方程![]() 的根
的根![]() 函数
函数![]() 与
与![]() 的交点.
的交点.
【题型】单选题
【结束】
13
【题目】设集合A={0,log3(a+1)},B={a,a+b}若A∩B={1},则b=______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com