
【题目】选修4-4:坐标系与参数方程
极坐标系中, ![]() 为极点,半径为2的圆
为极点,半径为2的圆![]() 的圆心坐标为
的圆心坐标为![]() .
.
(1)求圆![]() 的极坐标方程;
的极坐标方程;
(2)设直角坐标系的原点与极点![]() 重合,
重合, ![]() 轴非负关轴与极轴重合,直线
轴非负关轴与极轴重合,直线![]() 的参数方程为
的参数方程为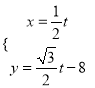 (
(![]() 为参数),由直线
为参数),由直线![]() 上的点向圆
上的点向圆![]() 引切线,求切线长的最小值.
引切线,求切线长的最小值.
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:
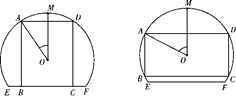
【题目】如图,一块弓形余布料EMF,点M为弧![]() 的中点,其所在圆O的半径为4 dm(圆心O在弓形EMF内),∠EOF=
的中点,其所在圆O的半径为4 dm(圆心O在弓形EMF内),∠EOF=![]() .将弓形余布料裁剪成尽可能大的矩形ABCD(不计损耗), AD∥EF,且点A、D在弧
.将弓形余布料裁剪成尽可能大的矩形ABCD(不计损耗), AD∥EF,且点A、D在弧![]() 上,设∠AOD=
上,设∠AOD=![]() .
.
(1)求矩形ABCD的面积S关于![]() 的函数关系式;
的函数关系式;
(2)当矩形ABCD的面积最大时,求cos![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在半径为2,圆心角为 ![]() 的扇形金属材料中剪出一个四边形MNQP,其中M、N两点分別在半径OA、OB上,P、Q两点在弧
的扇形金属材料中剪出一个四边形MNQP,其中M、N两点分別在半径OA、OB上,P、Q两点在弧 ![]() 上,且OM=ON,MN∥PQ.
上,且OM=ON,MN∥PQ. 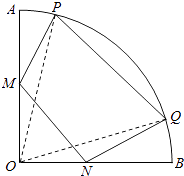
(1)若M、N分別是OA、OB中点,求四边形MNQP面积的最大值.
(2)PQ=2,求四边形MNQP面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班有24名男生和26名女生,数据a1 , a2 , …,a50是该班50名学生在一次数学学业水平模拟考试的成绩,下面的程序用来同时统计全班成绩的平均数:A,男生平均分:M,女生平均分:W;为了便于区别性别,输入时,男生的成绩用正数,女生的成绩用其成绩的相反数,那么在图里空白的判断框和处理框中,应分别填入下列四个选项中的( ) 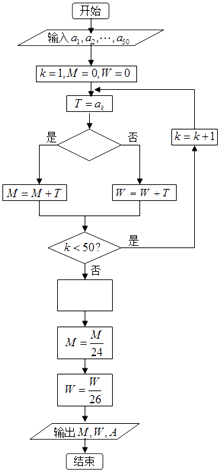
A.T>0?, ![]()
B.T<0?, ![]() ??
??
C.T<0?, ![]()
D.T>0?, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:关于x的不等式|x﹣2|+|x+2|>m的解集是R; q:关于x的不等式x2+mx+4>0的解集是R.则p成立是q成立的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.即不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,已知BC=1,BB1=2,∠BCC1=90°,AB⊥侧面BB1CC1 . 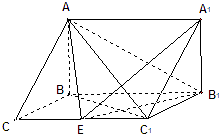
(1)求直线C1B与底面ABC所成角的正弦值;
(2)在棱CC1(不包含端点C,C1)上确定一点E的位置,使得EA⊥EB1(要求说明理由).
(3)在(2)的条件下,若AB= ![]() ,求二面角A﹣EB1﹣A1的大小.
,求二面角A﹣EB1﹣A1的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com