【题目】某研究机构为了了解各年龄层对高考改革方案的关注程度，随机选取了200名年龄在
内的市民进行了调查，并将结果绘制成如图所示的频率分布直方图（分第一～五组区间分别为
，
，
，
，
，
）.
（1）求选取的市民年龄在内的人数；
（2）若从第3,4组用分层抽样的方法选取5名市民进行座谈，再从中选取2人在座谈会中作重点发言，求作重点发言的市民中至少有一人的年龄在内的概率.
【答案】（1）20；（2）
【解析】
（1）选取的市民年龄在
内的频率，即可求出人数；
（2）利用分层抽样的方法从第3组选3，记为A1，A2，A3从第4组选2人，记为B1，B2；再利用古典概型的概率计算公式即可得出.
（1）由题意可知，年龄在内的频率为
，
故年龄在内的市民人数为
.
（2）易知，第3组的人数，第4组人数都多于20，且频率之比为
，
所以用分层抽样的方法在第3、4两组市民抽取5名参加座谈，
所以应从第3,4组中分别抽取3人，2人.
记第3组的3名分别为
，
，
，第4组的2名分别为
，
，则从5名中选取2名作重点发言的所有情况为
，
，
，
，
，
，
，
，
，
，共有10种.
其中第4组的2名，至少有一名被选中的有：，，，，，，，共有7种，所以至少有一人的年龄在
内的概率为.
寒假天地重庆出版社系列答案科目：高中数学 来源： 题型：
【题目】如图所示,ABCD是边长为60 cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得ABCD四个点重合于图中的点P, 正好形成一个正四棱柱形状的包装盒,若要包装盒容积V(cm3)最大, 则EF长为____ cm ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】[选修4-4：坐标系与参数方程]
在极坐标系中，曲线
的极坐标方程是
，以极点为原点
，极轴为
轴正半轴（两坐标系取相同的单位长度）的直角坐标系
中，曲线
的参数方程为： 
（
为参数）.
（1）求曲线
的直角坐标方程与曲线
的普通方程；
（2）将曲线
经过伸缩变换
后得到曲线
，若
， 
分别是曲线
和曲线
上的动点，求
的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，点A(0，3)，直线l：y＝2x－4，设圆C的半径为1，圆心C在直线l上，若圆C上存在点M，使|MA|＝2|MO|，则点M的轨迹方程是________，圆心C的横坐标的取值范围是________.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某机构通过对某企业2018年的前三个季度生产经营情况的调查，得到每月利润
（单位：万元）与相应月份数
的部分数据如表：
| 3 | 6 | 9 |
| 241 | 244 | 229 |
（1）根据上表数据，请从下列三个函数中选取一个恰当的函数描述与x的变化关系，并说明理由：
，
，
（2）利用（1）中选择的函数：
①估计月利润最大的是第几个月，并求出该月的利润；
②预估年底12月份的利润是多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在如图所示的多面体中，
平面
，
平面，
，且
，
是
的中点.
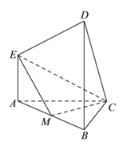
（1）求证：
；
（2）求平面
与平面
所成的二面角的正弦值；
（3）在棱
上是否存在一点
，使得直线
与平面所成的角是
. 若存在，指出点的位置；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了解男性家长和女性家长对高中学生成人礼仪式的接受程度，某中学团委以问卷形式调查了
位家长，得到如下统计表：
（1）据此样本，能否有
的把握认为“接受程度”与家长性别有关？说明理由；
（2）学校决定从男性家长中按分层抽样方法选出
人参加今年的高中学生成人礼仪式，并从中选
人交流发言，设
是发言人中持“赞成”态度的人数，求
的分布列及数学期望.
参考数据
|
|
|
|
|
|
参考公式
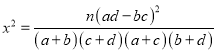
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
