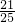Question

袋中有3个白球，2个红球共5个球．
（1）若有放回地依次取出两个球，求取得的两个球中至少有一个是白球的概率．
（2）若摸到白球时得1分，摸到红球时得2分，求任意取出3个球所得总分为5的概率．

Answer 1

解：（1）有放回地依次取出两个球，所有的取法有5×5=25种
取得的两个球中没有白球的取法有2×2=4种
∴取得的两个球中至少有一个是白球的取法有25-4=21种
由古典概型的概率公式得取得的两个球中至少有一个是白球的概率为
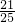
（2）任意取出3个球所得总分为5即摸出2个红球一个白球
∵任意取出3个球所有的取法有C₅³=10
摸出2个红球一个白球D的取法有C₂²•C₃¹=3
由古典概型的概率公式得
∴任意取出3个球所得总分为5的概率
分析：（1）利用分布乘法计数原理求出有放回地依次取出两个球所有的取法，再求出取得的两个球中至少有一个是白球，利用古典概型的概率公式求出概率．
（2）利用组合的方法求出任意取出3个球所有的取法，再求出任意取出3个球所得总分为5的取法，利用古典概型的概率公式求出概率．
点评：求事件的概率一个先判断出事件的概型，再选择合适的公式；利用古典概型的概率公式求事件的概率，关键是求出基本事件的方法数，求基本事件的方法数的方法有：列举法、列表法、排列组合的方法、树状图的方法．