
【题目】已知函数![]() ,
, ![]() .
.
(I)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)![]() ,使不等式
,使不等式![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2)![]()
【解析】试题分析:(Ⅰ)根据导数与单调性的关系可知增区间为![]() 的解集与定义域的交集,减区间为
的解集与定义域的交集,减区间为![]() 与定义域的交集;(Ⅱ)先将不等式变形化简得
与定义域的交集;(Ⅱ)先将不等式变形化简得![]() ,构造函数
,构造函数![]() ,问题转化为
,问题转化为![]() (如果是对任意的x恒成立则转化为
(如果是对任意的x恒成立则转化为![]() ),利用函数的单调性与极值求出函数h(x)的最大值得到问题的解.
),利用函数的单调性与极值求出函数h(x)的最大值得到问题的解.
试题解析:(Ⅰ)∵![]() 1分
1分
当a≤0时, ![]() 恒成立,f(x)在R上单调递减; 3分
恒成立,f(x)在R上单调递减; 3分
当a>0时,令![]() ,解得x=lna,
,解得x=lna,
由![]() 得f(x)的单调递增区间为
得f(x)的单调递增区间为![]() ;
;
由![]() 得f(x)的单调递减区间为
得f(x)的单调递减区间为![]() 5分
5分
(Ⅱ)因为![]() ,使不等式
,使不等式![]() ,则
,则![]() ,即
,即![]() ,
,
设![]() ,则问题转化为
,则问题转化为![]() , 8分
, 8分
由![]() ,令
,令![]() ,则
,则![]() ,
,
当x在区间![]() 内变化时,
内变化时, ![]() 变化情况如下表:
变化情况如下表:
x |
|
|
|
| + | 0 | - |
h(x) |
|
|
|
由上表可得,当x=![]() 时,函数h(x)有最大值,且最大值为
时,函数h(x)有最大值,且最大值为![]() ,
,
所以a≤![]() 12分
12分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知A=B=R,x∈A,y∈B,f:x→y=ax+b是从A到B的映射,若1和8的原象分别是3和10,则5在f下的象是( )
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得 ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)求家庭的月储蓄y对月收入x的线性回归方程y=bx+a;
(Ⅱ)判断变量x与y之间是正相关还是负相关;
(Ⅲ)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:线性回归方程y=bx+a中, 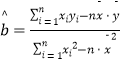 ,
, ![]() ,其中
,其中 ![]() ,
, ![]() 为样本平均值,线性回归方程也可写为
为样本平均值,线性回归方程也可写为 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为实常数.
为实常数.
(1)设![]() ,当
,当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,直线
时,直线![]() 、
、![]() 与函数
与函数![]() 的图象一共有四个不同的交点,且以此四点为顶点的四边形恰为平行四边形.求证:
的图象一共有四个不同的交点,且以此四点为顶点的四边形恰为平行四边形.求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,点P在正方形ABCD所在平面外,PA⊥平面ABCD,PA=AB,则PB与AC所成的角是( ) 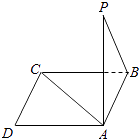
A.90°
B.60°
C.45°
D.30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合U={x|x是小于6的正整数},A={1,2},B∩(C∪A)={4},则∪(A∪B)=( )
A.{3,5}
B.{3,4}
C.{2,3}
D.{2,4}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面上两点A(﹣1,0),B(1,0),在圆C:(x﹣3)2+(y﹣4)2=4上取一点P,
(Ⅰ)x﹣y+c≥0恒成立,求c的范围
(Ⅱ)从x+y+1=0上的点向圆引切线,求切线长的最小值
(Ⅲ)求|PA|2+|PB|2的最值及此时点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
1)已知两平面的法向量分别为 ![]() =(0,1,0),
=(0,1,0), ![]() =(0,1,1),则两平面所成的二面角为45°或135°;
=(0,1,1),则两平面所成的二面角为45°或135°;
2)若曲线 ![]() +
+ ![]() =1表示双曲线,则实数k的取值范围是(﹣∞,﹣4)∪(1,+∞);
=1表示双曲线,则实数k的取值范围是(﹣∞,﹣4)∪(1,+∞);
3)已知双曲线方程为x2﹣ ![]() =1,则过点P(1,1)可以作一条直线l与双曲线交于A,B两点,使点P是线段AB的中点.
=1,则过点P(1,1)可以作一条直线l与双曲线交于A,B两点,使点P是线段AB的中点.
其中正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为坐标原点,F是椭圆C: ![]() =1(a>b>0)的左焦点,A,B分别为C的左,右顶点.P为C上一点,且PF⊥x轴,过点A的直线l与线段PF交于点M,与y轴交于点E.若直线BM经过OE的中点,则C的离心率为( )
=1(a>b>0)的左焦点,A,B分别为C的左,右顶点.P为C上一点,且PF⊥x轴,过点A的直线l与线段PF交于点M,与y轴交于点E.若直线BM经过OE的中点,则C的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com