
设 是首项为a,公差为d的等差数列
是首项为a,公差为d的等差数列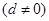 ,
, 是其前n项的和。记
是其前n项的和。记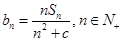 ,其中c为实数。
,其中c为实数。
(1)若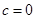 ,且
,且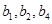 成等比数列,证明:
成等比数列,证明: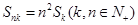 ;
;
(2)若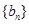 是等差数列,证明:
是等差数列,证明: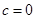 。
。
(1)见解析(2)见解析
解析试题分析:
(1)根据题意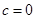 时,可得
时,可得 ,即得到
,即得到 通项,则可根据
通项,则可根据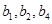 成等比数列,得到
成等比数列,得到 关系,从而将
关系,从而将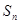 化为关于
化为关于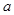 的式子.进而证明结论.
的式子.进而证明结论.
(2) 根据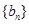 是等差数列,可设出
是等差数列,可设出 ,则有
,则有 ,将
,将 代入,化简该式为
代入,化简该式为 样式,通过令
样式,通过令 ,建立方程组,可解得
,建立方程组,可解得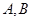 .则可讨论出
.则可讨论出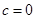 .
.
试题解析:
由题意可知 .①
.①
(1)由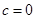 ,得
,得 .
.
又因为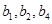 成等比数列,所以
成等比数列,所以 ,
,
即 ,化简得
,化简得 .
.
因为 ,所以
,所以 .因此对于所有的
.因此对于所有的 ,①有
,①有 .
.
从而对于所有的 ,有
,有 。
。
(2)设数列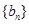 的公差为
的公差为 ,则
,则 ,
,
即 ,代入
,代入 的表达式,整理得,对于所有的
的表达式,整理得,对于所有的 ,
,
有 .
.
令 ,
,
则对于所有的 ,有
,有 .(*)
.(*)
在(*)式中分别取 ,得
,得 ,
,
从而有 ①,
①, ②,
②, ③,
③,
由②③得 ,代入方程①,得
,代入方程①,得 ,从而
,从而 .
.
即 ,
, 。
。
若 ,则由
,则由 ,得
,得 ,与题设矛盾,所以
,与题设矛盾,所以 。
。
又因为 ,所以
,所以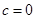 。
。
考点:等差数列前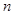 项和,等比中项;化繁为简的思想,等价代换的思想.
项和,等比中项;化繁为简的思想,等价代换的思想.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
(2011•湖北)已知数列{an}的前n项和为Sn,且满足:a1=a(a≠0),an+1=rSn(n∈N*,r∈R,r≠﹣1).
(1)求数列{an}的通项公式;
(2)若存在k∈N*,使得Sk+1,Sk,Sk+2成等差数列,试判断:对于任意的m∈N*,且m≥2,am+1,am,am+2是否成等差数列,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列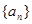 满足
满足 (
( ).
).
(1)若数列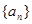 是等差数列,求它的首项和公差;
是等差数列,求它的首项和公差;
(2)证明:数列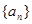 不可能是等比数列;
不可能是等比数列;
(3)若 ,
, (
( ),试求实数
),试求实数 和
和 的值,使得数列
的值,使得数列 为等比数列;并求此时数列
为等比数列;并求此时数列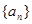 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知公比不为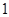 的等比数列
的等比数列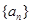 的首项
的首项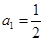 ,前
,前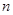 项和为
项和为 ,且
,且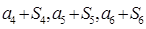 成等差数列.
成等差数列.
(1)求等比数列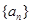 的通项公式;
的通项公式;
(2)对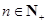 ,在
,在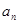 与
与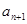 之间插入
之间插入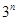 个数,使这
个数,使这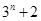 个数成等差数列,记插入的这
个数成等差数列,记插入的这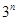 个数的和为
个数的和为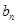 ,求数列
,求数列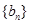 的前
的前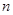 项和
项和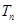 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com