练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】若函数y=f（x）是定义在R上的奇函数，且在区间（﹣∞，0]上是减函数，则不等式f（lnx）＜﹣f（1）的解集为（ ）
    A.（e，+∞）
    B.（ ，+∞）
    C.（ ，e）
    D.（0， ）

    【答案】B
    【解析】解：函数y=f（x）是定义在R上的奇函数，且在区间（﹣∞，0]上是减函数， ∴f（x）在（0，+∞）上也是减函数，故函数f（x）在R上单调递减．
    不等式f（lnx）＜﹣f（1），即不等式f（lnx）＜f（﹣1），
    ∴lnx＞﹣1，x＞ ，
    故选：B．
    【考点精析】本题主要考查了奇偶性与单调性的综合的相关知识点，需要掌握奇函数在关于原点对称的区间上有相同的单调性；偶函数在关于原点对称的区间上有相反的单调性才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在 中， .

    （1）求 与 的面积之比；
    （2）若 为 中点， 与 交于点 ，且 ，求 的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】和谐高级中学共有学生570名，各班级人数如表：

    一班

    二班

    三班

    四班

    高一

    52

    51

    y

    48

    高二

    48

    x

    49

    47

    高三

    44

    47

    46

    43

    已知在全校学生中随机抽取1名，抽到高二年级学生的概率是 ．
    （1）求x，y的值；
    （2）现用分层抽样的方法在全校抽取114名学生，应分别在各年级抽取多少名？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某圆拱桥的示意图如图所示，该圆拱的跨度AB是36 m，拱高OP是6 m，在建造时，每隔3 m需用一个支柱支撑，求支柱A2P2的长．(精确到0.01 m)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系xoy中，动点M到点F（1，0）的距离与它到直线x=2的距离之比为 ． （Ⅰ）求动点M的轨迹E的方程；
    （Ⅱ）设直线y=kx+m（m≠0）与曲线E交于A，B两点，与x轴、y轴分别交于C，D两点（且C，D在A，B之间或同时在A，B之外）．问：是否存在定值k，对于满足条件的任意实数m，都有△OAC的面积与△OBD的面积相等，若存在，求k的值；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知命题p：关于x的不等式x2+（a﹣1）x+1≤0的解集为；命题q：方程 表示焦点在y轴上的椭圆；若命题q为真命题，p∨q为真命题．
    （1）求实数a的取值范围；
    （2）判断方程（a+1）x2+（1﹣a）y2=（a+1）（1﹣a）所表示的曲线的形状．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}的前n项和为Sn ， 且满足a1=3，Sn+1=3（Sn+1）（n∈N*）． （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）在数列{bn}中，b1=9，bn+1﹣bn=2（an+1﹣an）（n∈N*），若不等式λbn＞an+36（n﹣4）+3λ对一切n∈N*恒成立，求实数λ的取值范围；
    （Ⅲ）令Tn= + + +…+ （n∈N*），证明：对于任意的n∈N* ， Tn＜ ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某城市随机抽取一个月（30天）的空气质量指数API监测数据，统计结果如下：

    API

    [0，50]

    （50，100]

    （100，150]

    （150，200]

    （200，250]

    （250，300]

    （300，350]

    空气质量

    优

    良

    轻微污染

    轻度污染

    中度污染

    中度重污染

    重度污染

    天数

    2

    4

    5

    9

    4

    3

    3

    （Ⅰ）根据以上数据估计该城市这30天空气质量指数API的平均值；
    （Ⅱ）若该城市某企业因空气污染每天造成的经济损失S（单位：元）与空气质量指数API（记为w）的关系式为：
    S=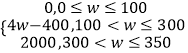
    若在本月30天中随机抽取一天，试估计该天经济损失S大于200元且不超过600元的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知： ；
    ；
    ，
    利用上述结果，计算：13+23+33+…+n3= ．

    查看答案和解析>>

    同步练习册答案