
【题目】定义:已知函数f(x)在[m,n](m<n)上的最小值为t,若t≤m恒成立,则称函数f(x)在[m,n](m<n)上具有“DK”性质.例如函数 ![]() 在[1,9]上就具有“DK”性质.
在[1,9]上就具有“DK”性质.
(1)判断函数f(x)=x2﹣2x+2在[1,2]上是否具有“DK”性质?说明理由;
(2)若g(x)=x2﹣ax+2在[a,a+1]上具有“DK”性质,求a的取值范围.
【答案】
(1)解:∵f(x)=x2﹣2x+2,x∈[1,2],
对称轴x=1,开口向上.
当x=1时,取得最小值为f(1)=1,
∴f(x)min=f(1)=1≤1,
∴函数f(x)在[1,2]上具有“DK”性质
(2)解:g(x)=x2﹣ax+2,x∈[a,a+1],其图象的对称轴方程为 ![]() .
.
①当 ![]() ,即a≥0时,
,即a≥0时, ![]() .
.
若函数g(x)具有“DK”性质,则有2≤a总成立,即a≥2.
②当 ![]() ,即﹣2<a<0时,
,即﹣2<a<0时, ![]() .
.
若函数g(x)具有“DK”性质,则有 ![]() 总成立,解得a无解.
总成立,解得a无解.
③当 ![]() ,即a≤﹣2时,g(x)min=g(a+1)=a+3.
,即a≤﹣2时,g(x)min=g(a+1)=a+3.
若函数g(x)具有“DK”性质,则有a+3≤a,解得a无解.
综上所述,若g(x)=x2﹣ax+2在[a,a+1]上具有“DK”性质,则a≥2
【解析】(1)直接根据新定义进行判断即可.(2)根据二次函数的性质,求出对称轴,对其进行讨论,根据新定义求解.


科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知椭圆![]() 过点A(2,1),离心率为
过点A(2,1),离心率为![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线![]() 与椭圆相交于B,C两点(异于点A),线段BC被y轴平分,且
与椭圆相交于B,C两点(异于点A),线段BC被y轴平分,且![]() ,求直线l的方程.
,求直线l的方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.

(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知椭圆的左焦点为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() ,
,![]() (
(![]() 都在
都在![]() 轴上方),且
轴上方),且![]() .
.
(ⅰ)若![]() ,求
,求![]() 的面积;
的面积;
(ⅱ)直线![]() 是否恒过定点?若过定点,求出该定点的坐标;若不过定点,请说明理由.
是否恒过定点?若过定点,求出该定点的坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
平面直角坐标系中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的极坐标方程与曲线
的极坐标方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知与直线![]() 平行的直线
平行的直线![]() 过点
过点![]() ,且与曲线
,且与曲线![]() 交于
交于![]() 两点,试求
两点,试求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但采集上市时蔬菜仍存有少量的残留农药,食用时需要用清水清洗干净,下表是用清水![]() (单位:千克)清洗该蔬菜1千克后,蔬菜上残留的农药
(单位:千克)清洗该蔬菜1千克后,蔬菜上残留的农药![]() (单位:微克)的统计表:
(单位:微克)的统计表:

(1)令![]() ,利用给出的参考数据求出
,利用给出的参考数据求出![]() 关于
关于![]() 的回归方程
的回归方程![]() .(
.(![]() ,
,![]() 精确到0.1)
精确到0.1)
参考数据:![]() ,
,![]() ,
,![]()
其中![]() ,
,![]()
(2)对于某种残留在蔬菜上的农药,当它的残留量不高于20微克时对人体无害,为了放心食用该蔬菜,请估计至少需用用多少千克的清水清洗1千克蔬菜?(精确到0.1,参考数据![]() )
)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为
 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,集合A={x|x<﹣2或3<x≤4},B={x|x2﹣2x﹣15≤0}.求:
(1)UA;
(2)A∪B;
(3)若C={x|x>a},且B∩C=B,求a的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
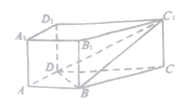
【题目】如图,四棱柱![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 是梯形,
是梯形,![]() ,
,![]() ,
,![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ,若存在,请确定点
,若存在,请确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节油降耗技术发行后生产甲产品过程中记录的产量 x (吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出 y 关于 x 的线性回归方程![]()
(3)已知该厂技改前 100 吨甲产品的生产能耗为 90 吨标准煤,试根据(2)求出的线性回归方程,预测生产100 吨甲产品的生产能耗比技改前降低多少吨标准煤?(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com