
| A. | 7π | B. | 9π | C. | 11π | D. | 13π |
分析 先求出圆M的半径,然后根据勾股定理求出OM的长,找出二面角的平面角,从而求出ON的长,最后利用垂径定理即可求出圆N的半径,从而求出面积.
解答  解:∵圆M的面积为4π,
解:∵圆M的面积为4π,
∴圆M的半径为2,
根据勾股定理可知OM=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∵过圆心M且与α成30°二面角的平面β截该球面得圆N,
∴∠OMN=60°,
在直角三角形OMN中,ON=2$\sqrt{3}×\frac{\sqrt{3}}{2}$=3,
∴圆N的半径为$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$,
∴圆N的面积为:7π.
故选:A.
点评 本题考查二面角的平面角,以及解三角形知识,同时考查空间想象能力,分析问题解决问题的能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
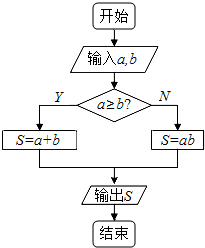 定义一种运算S=a?b,在如图所示的框图所表达的算法中揭示了这种运算“?”的含义,那么按照运算“?”的含义,S=tan60°?tan30°+cos60°?cos30°=( )
定义一种运算S=a?b,在如图所示的框图所表达的算法中揭示了这种运算“?”的含义,那么按照运算“?”的含义,S=tan60°?tan30°+cos60°?cos30°=( )| A. | $\frac{{3+\sqrt{3}}}{2}$ | B. | $\frac{{4+\sqrt{3}}}{4}$ | C. | $\frac{{19\sqrt{3}}}{12}$ | D. | $\frac{{11\sqrt{3}}}{6}+\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com