
ЈЁұҫРЎМвВъ·Ц12·ЦЈ©
ДіФ°БЦҫЦ¶Ф1000ЦкКчДҫөДЙъіӨЗйҝцҪшРРөчІйЈ¬ЖдЦРЙјКч 600ЦкЈ¬»ұКч400Цк .ПЦУГ·ЦІгійСщ·Ҫ·ЁҙУХв1000ЦкКчДҫЦРЛж»ъійИЎ100ЦкЈ¬ЙјКчУл»ұКчөДКчёЙЦЬіӨЈЁөҘО»ЈәcmЈ©өДійІйҪб№ыИзПВұнЈә
|
КчёЙЦЬіӨ ЈЁөҘО»Јәcm Ј© |
[30,40) |
[40,50) |
[50,60) |
[60,70) |
|
Йј Кч |
6 |
19 |
21 |
|
|
»ұ Кч |
4 |
20 |
|
6 |
(I)Зу Ј¬
Ј¬ Цөј°№АјЖ»ұКчКчёЙЦЬіӨөДЦЪКэЈ»
Цөј°№АјЖ»ұКчКчёЙЦЬіӨөДЦЪКэЈ»
ЈЁўтЈ©Из№ыЙјКчөДКчёЙЦЬіӨі¬№э60cmҫНҝЙТФҝі·ҘЈ¬Зл№АјЖёГЖ¬Ф°БЦҝЙТФҝі·ҘөДЙјКчУР¶аЙЩЦкЈҝ
ЈЁўуЈ©КчёЙЦЬіӨФЪ30cmөҪ40cmЦ®јдөД4Цк»ұКчУР1Цк»јіжәҰЈ¬ПЦТӘ¶ФХв4ЦкКчЦрТ»ҪшРРЕЕІйЦұЦБХТіц»јіжәҰөДКчДҫОӘЦ№.ЗуЕЕІйөДКчДҫЗЎәГОӘ2ЦкөДёЕВК.
ЈЁўсЈ©№АјЖ»ұКчКчёЙЦЬіӨөДЦЪКэОӘ45CM
ЈЁўтЈ©№АјЖёГЖ¬Ф°БЦҝЙТФҝі·ҘөДЙјКчУР140Цк
ЈЁўуЈ©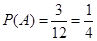
ЎҫҪвОцЎҝұҫКФМвЦчТӘКЗҝјІйБЛ№ЕөдёЕРНёЕВКөДЗуҪвЈ¬ТФј°ЖөКэөДОКМвЈ¬ТФј°ійСщ·Ҫ·ЁөДЧЫәПФЛУГЎЈ
ЈЁ1Ј©ТтОӘ°ҙ·ЦІгійСщ·Ҫ·ЁЛж»ъійИЎ100ЦкЈ¬ҝЙөГ»ұКчОӘ40Ј¬ЙјКч60Цк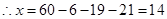 Ј¬
Ј¬ ҝЙЦӘ№АјЖ»ұКчөДЦЬіӨөДЦЪКэЎЈ
ҝЙЦӘ№АјЖ»ұКчөДЦЬіӨөДЦЪКэЎЈ
ЈЁ2Ј©ёщҫЭ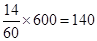 Ј¬№АјЖёГЖ¬Ф°БЦҝЙТФҝі·ҘөДЙјКчУР140Цк
Ј¬№АјЖёГЖ¬Ф°БЦҝЙТФҝі·ҘөДЙјКчУР140Цк
ЈЁ3Ј©ёщҫЭЙи4ЦкКчОӘ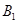 Ўў
Ўў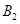 Ўў
Ўў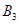 Ўў
Ўў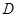 Ј¬Йи
Ј¬Йи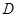 ОӘУРіжәҰөДДЗЦкЈ¬БРҫЩ·ЁөГөҪ»щұҫКВјюКэОӘ12ЦЦЈ¬¶шЙиКВјюA:ЕЕІйөДКчДҫЗЎәГОӘ2ЦкЈ¬КВјюA°ьә¬ЈЁ
ОӘУРіжәҰөДДЗЦкЈ¬БРҫЩ·ЁөГөҪ»щұҫКВјюКэОӘ12ЦЦЈ¬¶шЙиКВјюA:ЕЕІйөДКчДҫЗЎәГОӘ2ЦкЈ¬КВјюA°ьә¬ЈЁ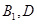 Ј©ЈЁ
Ј©ЈЁ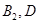 Ј©ЈЁ
Ј©ЈЁ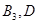 Ј©3ЦЦ
Ј©3ЦЦ
Ј¬ҝЙУГ№«КҪҪвөГЎЈ
ҪвЈәЈЁўсЈ©°ҙ·ЦІгійСщ·Ҫ·ЁЛж»ъійИЎ100ЦкЈ¬ҝЙөГ»ұКчОӘ40Ј¬ЙјКч60Цк
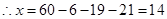 Ј¬
Ј¬ . №АјЖ»ұКчКчёЙЦЬіӨөДЦЪКэОӘ45CM
. №АјЖ»ұКчКчёЙЦЬіӨөДЦЪКэОӘ45CM
ЈЁўтЈ©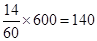 Ј¬№АјЖёГЖ¬Ф°БЦҝЙТФҝі·ҘөДЙјКчУР140Цк
Ј¬№АјЖёГЖ¬Ф°БЦҝЙТФҝі·ҘөДЙјКчУР140Цк
ЈЁўуЈ©Йи4ЦкКчОӘ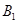 Ўў
Ўў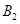 Ўў
Ўў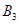 Ўў
Ўў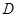 Ј¬Йи
Ј¬Йи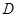 ОӘУРіжәҰөДДЗЦкЈ¬
ОӘУРіжәҰөДДЗЦкЈ¬
»щұҫКВјюОӘЈәЈЁ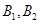 Ј©ЈЁ
Ј©ЈЁ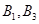 Ј©ЈЁ
Ј©ЈЁ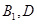 Ј©ЈЁ
Ј©ЈЁ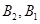 Ј©ЈЁ
Ј©ЈЁ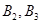 Ј©ЈЁ
Ј©ЈЁ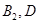 Ј©
Ј©
ЈЁ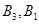 Ј©ЈЁ
Ј©ЈЁ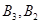 Ј©ЈЁ
Ј©ЈЁ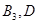 Ј©ЈЁ
Ј©ЈЁ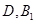 Ј©ЈЁ
Ј©ЈЁ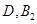 Ј©ЈЁ
Ј©ЈЁ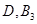 Ј©
Ј©
ЙиКВјюA:ЕЕІйөДКчДҫЗЎәГОӘ2ЦкЈ¬КВјюA°ьә¬ЈЁ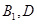 Ј©ЈЁ
Ј©ЈЁ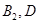 Ј©ЈЁ
Ј©ЈЁ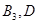 Ј©3ЦЦ
Ј©3ЦЦ



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
| 3 |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
| ON |
| ON |
| 5 |
| OM |
| OT |
| M1M |
| N1N |
| OP |
| OA |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЈЁұҫРЎМвВъ·Ц12·ЦЈ©ТСЦӘәҜКэ![]() Ј¬ЗТ
Ј¬ЗТ![]() ЎЈўЩЗу
ЎЈўЩЗу![]() өДЧоҙуЦөј°ЧоРЎЦөЈ»ўЪЗу
өДЧоҙуЦөј°ЧоРЎЦөЈ»ўЪЗу![]() өДФЪ¶ЁТеУтЙПөДөҘөчЗшјд.
өДФЪ¶ЁТеУтЙПөДөҘөчЗшјд.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЈЁ2009әюДПҫнОДЈ©ЈЁұҫРЎМвВъ·Ц12·ЦЈ©
ОӘАӯ¶ҜҫӯјГФціӨЈ¬ДіКРҫц¶ЁРВҪЁТ»ЕъЦШөг№ӨіМЈ¬·ЦұрОӘ»щҙЎЙиК©№ӨіМЎўГсЙъ№ӨіМәНІъТөҪЁЙи№ӨіМИэАаЈ¬ХвИэАа№ӨіМЛщә¬ПоДҝөДёцКэ·ЦұрХјЧЬКэөД![]() Ўў
Ўў![]() Ўў
Ўў![]() .ПЦУР3Гы№ӨИЛ¶АБўөШҙУЦРИОСЎТ»ёцПоДҝІОУлҪЁЙи.ЗуЈә
.ПЦУР3Гы№ӨИЛ¶АБўөШҙУЦРИОСЎТ»ёцПоДҝІОУлҪЁЙи.ЗуЈә
ЈЁIЈ©ЛыГЗСЎФсөДПоДҝЛщКфАаұр»ҘІ»ПаН¬өДёЕВКЈ» w.w.w.k.s.5.u.c.o.m ![]()
![]()
ЈЁIIЈ©ЦБЙЩУР1ИЛСЎФсөДПоДҝКфУЪГсЙъ№ӨіМөДёЕВК.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЈЁұҫРЎМвВъ·Ц12·ЦЈ©
ДіГсУӘЖуТөЙъІъAЈ¬BБҪЦЦІъЖ·Ј¬ёщҫЭКРіЎөчІйәНФӨІвЈ¬AІъЖ·өДАыИуУлН¶ЧКіЙХэұИЈ¬Жд№ШПөИзНј1Ј¬BІъЖ·өДАыИуУлН¶ЧКөДЛгКхЖҪ·ҪёщіЙХэұИЈ¬Жд№ШПөИзНј2Ј¬
ЈЁЧўЈәАыИуУлН¶ЧКөҘО»КЗНтФӘЈ©
ЈЁ1Ј©·ЦұрҪ«AЈ¬BБҪЦЦІъЖ·өДАыИуұнКҫОӘН¶ЧКөДәҜКэЈ¬ІўРҙіцЛьГЗөДәҜКэ№ШПөКҪ.ЈЁ2Ј©ёГЖуТөТСіпјҜөҪ10НтФӘЧКҪрЈ¬ІўИ«ІҝН¶ИлөҪAЈ¬BБҪЦЦІъЖ·өДЙъІъЈ¬ОКЈәФхСщ·ЦЕдХв10НтФӘН¶ЧКЈ¬ІЕДЬК№ЖуТө»сөГЧоҙуАыИуЈ¬ЖдЧоҙуАыИуОӘ¶аЙЩНтФӘ.
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com