
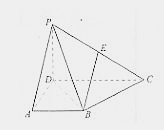
【题目】在四棱锥P—ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,E为PC中点,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,CD=2.
(Ⅰ)求证:BE∥平面PAD;
(Ⅱ)求证:BC⊥平面PBD;
(Ⅲ)设Q为侧棱PC上一点,![]() 试确定
试确定![]() 的值,使得二面角Q—BD—P为45°.
的值,使得二面角Q—BD—P为45°.
【答案】(Ⅰ)略
(Ⅱ)略
(Ⅲ)![]()
【解析】
解:(1)取PD的中点F,连接EF,AF,
因为E为PC中点,所以EF//CD,且![]() ,
,
在梯形ABCD中,AB//CD,AB=1,
所以EF//AB,EF=AB,四边形ABEF为平行四边形,
所以BE//AF,
BE![]() 平面PAD,AF
平面PAD,AF![]() 平面PAD,
平面PAD,
所以BE//平面PAD.
(2)平面PCD⊥底面ABCD,PD⊥CD,

所以PD⊥平面ABCD,
所以PD⊥AD.
如图,以D为原点建立空间直角坐标系Dxyz.
则A(1,0,0),B(1,1,0),C(0,2,0),P(0,0,1)
![]()
所以![]()
又由PD⊥平面ABCD,可得PD⊥BC,
所以BC⊥平面PBD.

(3)平面PBD的法向量为![]() =(-1,1,0)
=(-1,1,0)
![]()
所以Q![]()
设平面QBD的法向量为![]()
则![]() ,
,
所以![]() ,
,
所以
注意到![]()


科目:高中数学 来源: 题型:
【题目】 设椭圆![]() 的左焦点为
的左焦点为![]() ,左顶点为
,左顶点为![]() ,顶点为B.已知
,顶点为B.已知![]() (
(![]() 为原点).
为原点).
(Ⅰ)求椭圆的离心率;
(Ⅱ)设经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆在
与椭圆在![]() 轴上方的交点为
轴上方的交点为![]() ,圆
,圆![]() 同时与
同时与![]() 轴和直线
轴和直线![]() 相切,圆心
相切,圆心![]() 在直线
在直线![]() 上,且
上,且![]() ,求椭圆的方程.
,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A,B是半径为2的圆周上的定点,P为圆周上的动点,![]() 是锐角,大小为β.图中阴影区域的面积的最大值为
是锐角,大小为β.图中阴影区域的面积的最大值为
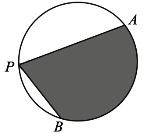
A. 4β+4cosβB. 4β+4sinβC. 2β+2cosβD. 2β+2sinβ
查看答案和解析>>
科目:高中数学 来源: 题型:
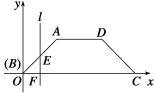
【题目】如图所示,已知底角为45°的等腰梯形ABCD,底边BC长为7 cm,腰长为2![]() cm,当一条垂直于底边BC(垂足为F)的直线l从B点开始由左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x(0≤x≤7),左边部分的面积为y,求y与x之间的函数关系式,画出程序框图,并写出程序.
cm,当一条垂直于底边BC(垂足为F)的直线l从B点开始由左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x(0≤x≤7),左边部分的面积为y,求y与x之间的函数关系式,画出程序框图,并写出程序.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设p:f(x)=1+ax,在(0,2]上f(x)≥0恒成立,q函数g(x)=ax+2lnx在其定义域上存在极值.
(1)若p为真命题,求实数a的取值范围;
(2)如果“p∨q”为真命题,“p∧q”为假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,一艺术拱门由两部分组成,下部为矩形![]() ,
,![]() 的长分别为
的长分别为![]() 和
和![]() ,上部是圆心为
,上部是圆心为![]() 的劣弧
的劣弧![]() ,
,![]() .
.
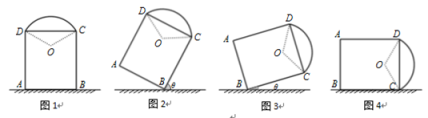
(1)求图1中拱门最高点到地面的距离;
(2)现欲以B点为支点将拱门放倒,放倒过程中矩形![]() 所在的平面始终与地面垂直,如图2、图3、图4所示.设
所在的平面始终与地面垂直,如图2、图3、图4所示.设![]() 与地面水平线
与地面水平线![]() 所成的角为
所成的角为![]() .记拱门上的点到地面的最大距离为
.记拱门上的点到地面的最大距离为![]() ,试用
,试用![]() 的函数表示
的函数表示![]() ,并求出
,并求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 分别是通过某城市开发区中心O的两条东西和南北走向的街道,连接M,N两地间的铁路是圆心在
分别是通过某城市开发区中心O的两条东西和南北走向的街道,连接M,N两地间的铁路是圆心在![]() 上的一段圆弧.若点M在点O正北方向,且
上的一段圆弧.若点M在点O正北方向,且![]() ,点N到
,点N到![]() ,
,![]() 的距离分别为5km和4km.
的距离分别为5km和4km.
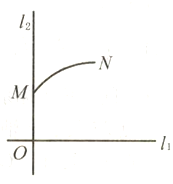
(1)建立适当的坐标系,求铁路路线所在圆弧的方程.
(2)若该城市的某中学拟在点O正东方向选址建分校,考虑环境问题,要求校址到点O的距离大于4km,并且铁路上任意一点到校址的距离不能小于![]() km,求该校址距点O的最近距离.
km,求该校址距点O的最近距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() 为抛物线
为抛物线![]() 外一点,过点
外一点,过点![]() 作抛物线
作抛物线![]() 的两条切线
的两条切线![]() ,
,![]() ,切点分别为
,切点分别为![]() ,
,![]() .
.
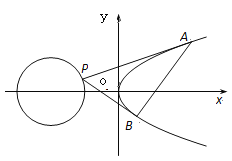
(Ⅰ)若点![]() 为
为![]() ,求直线
,求直线![]() 的方程;
的方程;
(Ⅱ)若点![]() 为圆
为圆![]() 上的点,记两切线
上的点,记两切线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com