
已知二次函数 .
.
(1)若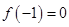 ,试判断函数
,试判断函数 零点个数;
零点个数;
(2)是否存在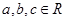 ,使
,使 同时满足以下条件
同时满足以下条件
①对任意 ,且
,且 ;
;
②对任意 ,都有
,都有 。若存在,求出
。若存在,求出 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
(3)若对任意 且
且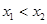 ,
, ,试证明存在
,试证明存在 ,
,
使 成立。
成立。
(1)函数 有两个零点。(2)当
有两个零点。(2)当 时,
时, 同时满足条件①、②. (3)利用零点存在性定理证明即可
同时满足条件①、②. (3)利用零点存在性定理证明即可
解析试题分析:(1)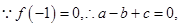
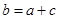
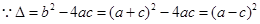 当
当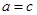 时
时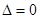 ,
,
函数 有一个零点; 3分
有一个零点; 3分
当 时,
时,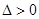 ,函数
,函数 有两个零点。 5分
有两个零点。 5分
(2)假设 存在,由①知抛物线的对称轴为x=-1,
存在,由①知抛物线的对称轴为x=-1,
∴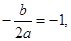 即
即 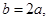 7分
7分
由②知对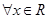 ,都有
,都有
令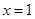 得
得
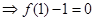
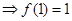
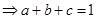 又因为
又因为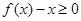 恒成立,
恒成立,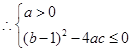
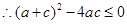 ,即
,即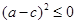 ,即
,即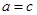
由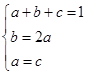 得
得 , 10分
, 10分
当 时,
时,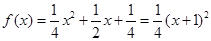 ,
,
其顶点为(-1,0)满足条件①,又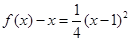
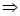 对
对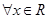 ,
,
都有 ,满足条件②.
,满足条件②.
∴存在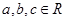 ,使
,使 同时满足条件①、②. .12分
同时满足条件①、②. .12分
(3)令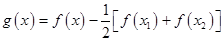 ,则
,则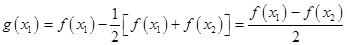
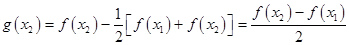 ,
,
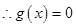 在
在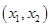 内必有一个实根。即
内必有一个实根。即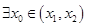 ,
,
使 成立 18分
成立 18分
考点:本题考查了函数的零点及恒成立问题
点评:①二次函数、一元二次方程和一元二次不等式是一个有机的整体,也是高考热点,要深刻理解它们相互之间的关系,能用函数思想来研究方程和不等式,便是抓住了关键.②二次函数 的图像形状、对称轴、顶点坐标、开口方向等是处理二次函数问题的重要依据.
的图像形状、对称轴、顶点坐标、开口方向等是处理二次函数问题的重要依据.


 精英口算卡系列答案
精英口算卡系列答案科目:高中数学 来源: 题型:解答题
作为绍兴市2013年5.1劳动节系列活动之一的花卉展在镜湖湿地公园举行.现有一占地1800平方米的矩形地块,中间三个矩形设计为花圃(如图),种植有不同品种的观赏花卉,周围则均是宽为1米的赏花小径,设花圃占地面积为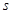 平方米,矩形一边的长为
平方米,矩形一边的长为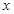 米(如图所示)
米(如图所示)
(1)试将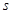 表示为
表示为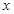 的函数;
的函数;
(2)问应该如何设计矩形地块的边长,使花圃占地面积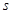 取得最大值.
取得最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
森林失火了,火正以 的速度顺风蔓延,消防站接到报警后立即派消防员前去,在失火后
的速度顺风蔓延,消防站接到报警后立即派消防员前去,在失火后 到达现场开始救火,已知消防队在现场每人每分钟平均可灭火
到达现场开始救火,已知消防队在现场每人每分钟平均可灭火 ,所消耗的灭火材料、劳务津贴等费用每人每分钟
,所消耗的灭火材料、劳务津贴等费用每人每分钟 元,另附加每次救火所损耗的车辆、器械和装备等费用平均每人
元,另附加每次救火所损耗的车辆、器械和装备等费用平均每人 元,而每烧毁
元,而每烧毁 森林的损失费为
森林的损失费为 元,设消防队派了
元,设消防队派了 名消防员前去救火,从到达现场开始救火到火全部扑灭共耗时
名消防员前去救火,从到达现场开始救火到火全部扑灭共耗时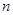
 .
.
(1)求出 与
与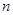 的关系式;
的关系式;
(2)问 为何值时,才能使总损失最小.
为何值时,才能使总损失最小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
2013年某工厂生产某种产品,每日的成本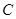 (单位:万元)与日产量
(单位:万元)与日产量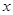 (单位:吨)满足函数关系式
(单位:吨)满足函数关系式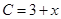 ,每日的销售额
,每日的销售额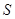 (单位:万元)与日产量
(单位:万元)与日产量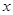 的函数关系式
的函数关系式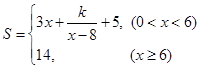
已知每日的利润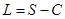 ,且当
,且当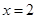 时,
时,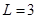 .
.
(1)求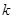 的值;
的值;
(2)当日产量为多少吨时,每日的利润可以达到最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某地方政府准备在一块面积足够大的荒地上建一如图所示的一个矩形综合性休闲广场,其总面积为3000平方米,其中场地四周(阴影部分)为通道,通道宽度均为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为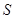 平方米.
平方米.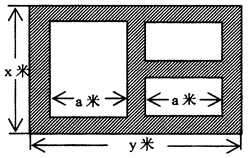
(1)分别写出用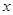 表示
表示 和用
和用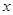 表示
表示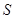 的函数关系式(写出函数定义域);
的函数关系式(写出函数定义域);
(2)怎样设计能使S取得最大值,最大值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
欲修建一横断面为等腰梯形(如图1)的水渠,为降低成本必须尽量减少水与渠壁的接触面,若水渠横断面面积设计为定值S,渠深h,则水渠壁的倾角α(0°<α<90°)应为多大时,方能使修建成本最低?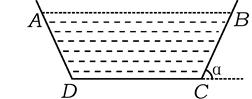
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com