练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

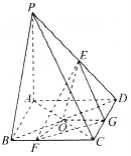
    【题目】如图所示，在底面为正方形的四棱锥P—ABCD中，AB=2，PA=4，PB=PD=，AC与BD相交于点O，E，G分别为PD，CD中点，

    (1)求证：EO//平面PBC；

    (2)设线段BC上点F满足BC=3BF，求三棱锥E—OFG的体积．

    【答案】（1）见解析（2）

    【解析】

    (1)由EO//PB，可证EO//平面PBC；

    （2）由勾股定理可证PA⊥AB,且PA⊥AD,故PA⊥面ABCD，E到底面的距离等于P点到底面距离的一半，再求出△FOG的面积，利用体积计算公式即可求解.

    （1）证明： E为PD中点，O为BD中点， EO 为△PBD中位线，EO//PB ,又 , , EO//平面PBC.

    （2） AB=2，PA=4，PB=PD= ，

    , ,同理可得.

    又 , 面ABCD，

    故P到面ABCD的距离为4，E到面ABCD的距离

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

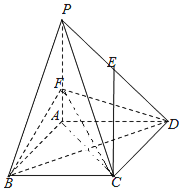
    【题目】在四棱锥中，底面ABCD是边长为6的菱形，且，平面ABCD，，F是棱PA上的一个动点，E为PD的中点．

    Ⅰ求证：．

    Ⅱ若．

    求PC与平面BDF所成角的正弦值；

    侧面PAD内是否存在过点E的一条直线，使得该直线上任一点M与C的连线，都满足平面BDF，若存在，求出此直线被直线PA、PD所截线段的长度，若不存在，请明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆C：x2+y2+2x﹣2y+1＝0和抛物线E：y2＝2px（p＞0），圆C与抛物线E的准线交于M、N两点，△MNF的面积为p，其中F是E的焦点．

    （1）求抛物线E的方程；

    （2）不过原点O的动直线l交该抛物线于A，B两点，且满足OA⊥OB，设点Q为圆C上任意一动点，求当动点Q到直线l的距离最大时直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，曲线C的方程为．以坐标原点为极点，轴正半轴为极轴建立极坐标系，直线的极坐标方程为．

    (1)求曲线C的参数方程和直线的直角坐标方程；

    (2)若直线与轴和y轴分别交于A，B两点，P为曲线C上的动点，求△PAB面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线的焦点为F，过F点的直线交抛物线于不同的两点A、B，且，点A关于轴的对称点为，线段的中垂线交轴于点D，则D点的坐标为

    A. (2，0)B. (3，0)C. (4，0)D. (5，0)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，曲线C的参数方程为 (其中为参数)，以坐标原点为极点，轴的正半轴为极轴建立极坐标系中，直线的极坐标方程为.

    （Ⅰ）求C的普通方程和直线的倾斜角；

    （Ⅱ）设点(0，2)，和交于两点，求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某高校随机抽取部分男生测试立定跳远，将成绩整理得到频率分布表如表，测试成绩在220厘米以上（含220厘米）的男生定为“合格生”，成绩在260厘米以上（含260厘米）的男生定为“优良生”．

    分组（厘米）

    频数

    频率

    [180，200）

    0.10

    [200，220）

    15

    [220，240）

    0.30

    [240，260）

    0.30

    [260，280）

    0.20

    合计

    1.00

    （1）求参加测试的男生中“合格生”的人数．

    （2）从参加测试的“合格生”中，根据表中分组情况，按分层抽样的方法抽取8名男生，再从这8名男生中抽取3名男生，记X表示3人中“优良生”的人数，求X的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥中，底面，，，，，点为棱的中点．

    （Ⅰ）证明：平面；

    （Ⅱ）求二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C：（a＞b＞0）的两个焦点分别为F1，F2，离心率为，过F1的直线l与椭圆C交于M，N两点，且△MNF2的周长为8．

    （1）求椭圆C的方程；

    （2）若直线y＝kx＋b与椭圆C分别交于A，B两点，且OA⊥OB，试问点O到直线AB的距离是否为定值，证明你的结论．

    查看答案和解析>>

    同步练习册答案