
【题目】如图y=f(x)的导函数的图象,现有四种说法:
(1)f(x)在(﹣3,1)上是增函数;
(2)x=﹣1是f(x)的极小值点;
(3)f(x)在(2,4)上是减函数,在(﹣1,2)上是增函数;
(4)x=2是f(x)的极小值点;
以上正确的序号为( )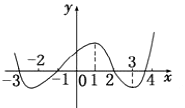
A.(1)(2)
B.(2)(3)
C.(3)(4)
D.(4)
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=(﹣x2+ax)ex , (x∈R,e为自然对数的底数)
(1)当a=2时,求函数f(x)的单调递增区间.
(2)函数f(x)是否为R上的单调函数,若是,求出a的取值范围;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x2+2ax,g(x)=3a2lnx+b,设两曲线y=f(x),y=g(x)有公共点,且在该点处的切线相同,则a∈(0,+∞)时,实数b的最大值是( )
x2+2ax,g(x)=3a2lnx+b,设两曲线y=f(x),y=g(x)有公共点,且在该点处的切线相同,则a∈(0,+∞)时,实数b的最大值是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量m=(3sinx,cosx),n=(-cosx,![]() cosx),f(x)=m·n-
cosx),f(x)=m·n-![]() .
.
(1)求函数f(x)的最大值及取得最大值时x的值;
(2)若方程f(x)=a在区间![]() 上有两个不同的实数根,求实数a的取值范围.
上有两个不同的实数根,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校拟建一块周长为400m的操场如图所示,操场的两头是半圆形,中间区域是矩形,学生做操一般安排在矩形区域,为了能让学生的做操区域尽可能大,试问如何设计矩形的长和宽? 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】放射性元素由于不断有原子放射出微粒子而变成其他元素,其含量不断减少,这种现象称为衰变.假设在放射性同位素铯137的衰变过程中,其含量M(单位:太贝克)与时间t(单位:年)满足函数关系:M(t)=M0 ![]() ,其中M0为t=0时铯137的含量.已知t=30时,铯137含量的变化率是﹣10In2(太贝克/年),则M(60)=( )
,其中M0为t=0时铯137的含量.已知t=30时,铯137含量的变化率是﹣10In2(太贝克/年),则M(60)=( )
A.5太贝克
B.75In2太贝克
C.150In2太贝克
D.150太贝克
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ax2﹣(2a+1)x+2lnx(a≥0)
ax2﹣(2a+1)x+2lnx(a≥0)
(1)当a=0时,求f(x)的单调区间;
(2)求y=f(x)在区间(0,2]上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)= ![]() 是定义在(﹣∞,+∞)上的奇函数,且f(
是定义在(﹣∞,+∞)上的奇函数,且f( ![]() )=
)= ![]() .
.
(1)求实数a、b,并确定函数f(x)的解析式;
(2)判断f(x)在(﹣1,1)上的单调性,并用定义证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com