练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．已知集合A={x∈N|x≤1}，B={x|-1≤x≤2}，则A∩B=（　　）
    A．{0，1}B．{-1，0，1}C．[-1，1]D．{1}

    分析 集合A与集合B的公共元素构成集合A∩B．

    解答 解：∵集合A={x∈N|x≤1}，B={x|-1≤x≤2}，∴A∩B={0，1}．
    故选A．

    点评 本题考查集合的交集及其运算，是基础题．解题时要认真审题，仔细解答，注意合理地进行等价转化．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    20．已知函数$f（x）=\left\{{\begin{array}{l}{{2^x}-a（x＜1）}\\{4（x-a）（x-2a）（x≥1）}\end{array}}\right.$．若f（x）=0恰有2个实数根，则实数a的取值范围是$[\frac{1}{2}，1）∪[2，+∞）$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．不等式$\frac{1}{x-1}$＜1的解集记为p，关于x的不等式x2+（a-1）x-a＞0的解集记为q，若p是q的充分不必要条件，则实数a的取值范围是（　　）
    A．（-2，-1]B．[-2，-1]C．（-∞，-2]∪[-1，+∞）D．（-∞，-2）∪（-1，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知α是三角形的内角，且sinα+cosα=-$\frac{1}{5}$，则tanα的值为（　　）
    A．$-\frac{4}{3}$B．$\frac{3}{4}$C．$-\frac{3}{4}$D．$-\frac{3}{4}$或$-\frac{4}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

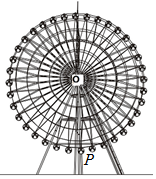    5．如图所示，游乐场中的摩天轮匀速逆时针旋转，每转一圈需要6min，其中心O距离地面40.5m，摩天轮的半径为40m，已知摩天轮上点P的起始位置在最低点处，在时刻t（min）时点P距离地面的高度为f（t）=Asin（ωt+φ）+h（A＞0，ω＞0，-π＜φ＜0，t≥0）．
    （Ⅰ）求f（t）的单调减区间；
    （Ⅱ）求证：f（t）+f（t+2）+f（t+4）是定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

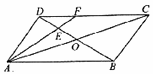
    15．在平行四边形ABCD中，AC与BD交于点O，E是线段OD的中点，AE的延长线与CD相交于点F，则$\overrightarrow{AF}$=（　　）
    A．$\frac{1}{4}\overrightarrow{AC}+\frac{1}{2}\overrightarrow{BD}$B．$\frac{1}{2}\overrightarrow{AC}+\frac{1}{4}\overrightarrow{BD}$C．$\frac{1}{2}\overrightarrow{AC}+\frac{2}{3}\overrightarrow{BD}$D．$\frac{2}{3}\overrightarrow{AC}+\frac{1}{3}\overrightarrow{BD}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．如图，在六面体ABCD-A1B1C1D1中，M，N分别是棱A1B1，B1C1的中点，平面ABCD⊥平面A1B1BA，平面ABCD平面B1BCC1．
    （1）证明：BB1⊥平面ABCD；
    （2）已知六面体ABCD-A1B1C1D1的棱长均为$\sqrt{5}$，cos∠BAD=$\frac{3}{5}$，设平面BMN与平面AB1D1相交所成二面角的大小为θ求cosθ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知抛物线y2=2px（p＞0）上一点M（1，y）到焦点F的距离为$\frac{17}{16}$．
    （1）求p的值；
    （2）若圆（x-a）2+y2=1与抛物线C有四个不同的公共点，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．定义：如果函数y=f（x）在定义域内给定区间[a，b]上存在x0（a＜x0＜b），满足f（x0）=$\frac{f（b）-f（a）}{b-a}$，则称函数y=f（x）是[a，b]上的“平均值函数”，x0是它的一个均值点，例如y=|x|是[-2，2]上的平均值函数，0就是它的均值点，若函数f（x）=x2-mx-1是[-1，1]上的“平均值函数”，则实数m的取值范围是（　　）
    A．[-1，1]B．（0，2）C．[-2，2]D．（0，1）

    查看答案和解析>>

    同步练习册答案