【答案】
分析:(1)设P(x,y),根据点到直线的距离公式和两点间的距离公式,建立关于x、y的方程并化简整理,即可得到曲线C
1的方程.分别取x=0和y=0解出曲线C
1在轴上的截距,即可曲线C
1与坐标轴的各交点的坐标.再由曲线是以F(
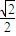
,
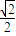
)为焦点,直线l
1:x+y+
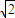
=0为准线的抛物线,将其顺时针方向旋转45°得到的抛物线焦点为(1,0),准线为x=-1,可得曲线C
2的方程是y
2=4x;
(2)设A(x
1,y
1)、B(x
2,y
2),直线l
2的方程为y=k(x-m),与抛物线y
2=4x消去x,得y
2-
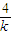
y-4m=0,可得y
1y
2=-4m.设N(-m,0),由

=λ
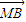
算出λ=

,结合向量坐标运算公式得到

-λ
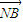
关于x
1、x
2、λ和m的坐标式,代入
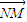
•(

-λ
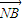
)并化简,整理可得
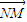
•(
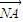
-λ
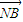
)=0,从而得到对任意的λ满足
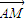
=λ

,都有
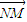
⊥(
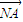
-λ
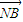
).
解答:解(1)设P(x,y),由题意知曲线C
1为抛物线,并且有

=
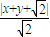
,
化简得抛物线C
1的方程为:x
2+y
2-2xy-4
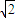
x-4

y=0.
令x=0,得y=0或y=4
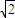
;再令y=0,得x=0或x=4
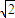
,
所以,曲线C
1与坐标轴的交点坐标为(0,0)、(0,4
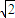
)和(4
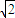
,0).
点F(

,
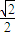
)到l
1:x+y+
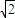
=0的距离为
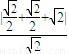
=2,
所以C
2是以(1,0)为焦点,以x=-1为准线的抛物线,其方程为:y
2=4x.
(2)设A(x
1,y
1),B(x
2,y
2),由题意知直线l
2的斜率k存在且不为零,
设直线l
2的方程为y=k(x-m),代入y
2=4x得
y
2-
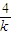
y-4m=0,可得y
1y
2=-4m.
由
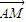
=λ

,得(m-x
1,-y
1)=λ(x
2-m,y
2),可得λ=

,
而N(-m,0),可得
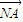
-λ
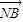
=(x
1+m,y
1)-λ(x
2+m,y
2)=(x
1-λx
2+(1-λ)m,y
1-λy
2)
∵
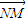
=(2m,0),
∴
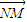
•(
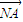
-λ

)=2m[x
1-λx
2+(1-λ)m]=2m[
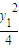
+
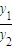
-

+(1+

)m]
=2m(y
1+y
2)•
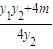
=2m(y
1+y
2)•
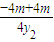
=0
∴对任意的λ满足
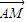
=λ

,都有

⊥(
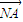
-λ
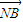
).
点评:本题给出动点的轨迹,求轨迹对应的方程并讨论由曲线产生的向量互相垂直的问题,着重考查了点到直线的距离公式、平面内两点的距离公式、一元二次方程根与系数的关系和平面向量数量积的坐标运算等知识,属于中档题.

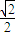 ,
,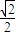 )的距离与到定直线l1:x+y+
)的距离与到定直线l1:x+y+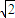 =0的距离相等的动点P的轨迹,曲线C2是由曲线C1绕坐标原点O按顺时针方向旋转45°形成的.
=0的距离相等的动点P的轨迹,曲线C2是由曲线C1绕坐标原点O按顺时针方向旋转45°形成的.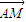 =λ
=λ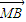 ,证明:
,证明: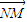 ⊥(
⊥(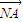 -λ
-λ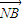 ).
).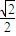 ,
,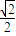 )为焦点,直线l1:x+y+
)为焦点,直线l1:x+y+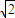 =0为准线的抛物线,将其顺时针方向旋转45°得到的抛物线焦点为(1,0),准线为x=-1,可得曲线C2的方程是y2=4x;
=0为准线的抛物线,将其顺时针方向旋转45°得到的抛物线焦点为(1,0),准线为x=-1,可得曲线C2的方程是y2=4x;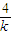 y-4m=0,可得y1y2=-4m.设N(-m,0),由
y-4m=0,可得y1y2=-4m.设N(-m,0),由 =λ
=λ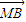 算出λ=
算出λ= ,结合向量坐标运算公式得到
,结合向量坐标运算公式得到 -λ
-λ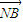 关于x1、x2、λ和m的坐标式,代入
关于x1、x2、λ和m的坐标式,代入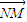 •(
•( -λ
-λ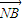 )并化简,整理可得
)并化简,整理可得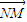 •(
•(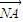 -λ
-λ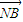 )=0,从而得到对任意的λ满足
)=0,从而得到对任意的λ满足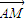 =λ
=λ ,都有
,都有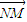 ⊥(
⊥(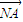 -λ
-λ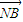 ).
). =
=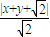 ,
,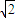 x-4
x-4 y=0.
y=0.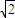 ;再令y=0,得x=0或x=4
;再令y=0,得x=0或x=4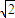 ,
,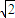 )和(4
)和(4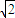 ,0).
,0). ,
,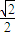 )到l1:x+y+
)到l1:x+y+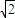 =0的距离为
=0的距离为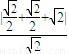 =2,
=2,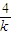 y-4m=0,可得y1y2=-4m.
y-4m=0,可得y1y2=-4m.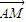 =λ
=λ ,得(m-x1,-y1)=λ(x2-m,y2),可得λ=
,得(m-x1,-y1)=λ(x2-m,y2),可得λ= ,
,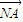 -λ
-λ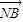 =(x1+m,y1)-λ(x2+m,y2)=(x1-λx2+(1-λ)m,y1-λy2)
=(x1+m,y1)-λ(x2+m,y2)=(x1-λx2+(1-λ)m,y1-λy2)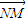 =(2m,0),
=(2m,0),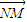 •(
•(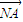 -λ
-λ )=2m[x1-λx2+(1-λ)m]=2m[
)=2m[x1-λx2+(1-λ)m]=2m[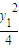 +
+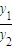 -
- +(1+
+(1+ )m]
)m]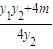 =2m(y1+y2)•
=2m(y1+y2)•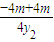 =0
=0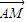 =λ
=λ ,都有
,都有 ⊥(
⊥(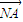 -λ
-λ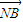 ).
).

 一本好题口算题卡系列答案
一本好题口算题卡系列答案 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是