
【题目】在三棱锥A﹣BCD中,点A在BD上的射影为O,∠BAD=∠BCD=90°,AB=BC=2,AD=DC=2 ![]() ,AC=
,AC= ![]() .
. 
(1)求证:AO⊥平面BCD;
(2)若E是AC的中点,求直线BE和平面BCD所成角的正切值.
【答案】
(1)证明:连接OC,由点A在BD上的射影为O,可得
AO⊥BD,
由∠BAD=∠BCD=90°,AB=BC=2,AD=DC=2 ![]() ,可得
,可得
BD= ![]() =4,AO=
=4,AO= ![]() =
= ![]() =
= ![]() ,
,
同理可得CO= ![]() ,由AO2+CO2=AC2,可得AO⊥CO,
,由AO2+CO2=AC2,可得AO⊥CO,
又BD,CO平面BCD,且BD,CO为相交二直线,
可得AO⊥平面BCD;
(2)解:取CO的中点H,连接EH,
由中位线定理可得EH∥AO,EH= ![]() AO,
AO,
由AO⊥平面BCD,可得EH⊥平面BCD,
即有∠EBH为直线BE和平面BCD所成角.
又EH= ![]() ,BE=
,BE= ![]() =
= ![]() =
= ![]() ,
,
BH= ![]() =
= ![]() =
= ![]() ,
,
可得tan∠EBH= ![]() =
= ![]() .
.
即有直线BE和平面BCD所成角的正切值为 ![]() .
.

【解析】(1)连接OC,由题意可得AO⊥BD,由勾股定理的逆定理可得AO⊥CO,运用线面垂直的判定定理,即可得证;(2)取CO的中点H,连接EH,运用中位线定理和线面垂直的性质定理,可得EH⊥平面BCD,即有∠EBH为直线BE和平面BCD所成角.运用正切函数的定义,计算即可得到所求值.
【考点精析】关于本题考查的直线与平面垂直的判定和空间角的异面直线所成的角,需要了解一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则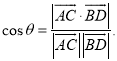 才能得出正确答案.
才能得出正确答案.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:
【题目】已知中心在原点O,焦点在x轴上的椭圆的一个顶点为B(0,1),B到焦点的距离为2. 
(1)求椭圆的标准方程;
(2)设P,Q是椭圆上异于点B的任意两点,且BP⊥BQ,线段PQ的中垂线l与x轴的交点为(x0 , 0),求x0的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义域为R的偶函数y=f(x)满足f(x+2)+f(x)=0,且当x∈[0,2]时,f(x)=2﹣x2 , 则方程f(x)=2sinx在[﹣3π,3π]内根的个数是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若实数x,y满足:x2+y2﹣2x﹣2y=0,则x+y的取值范围是( )
A.[﹣4,0]
B.[2﹣2 ![]() ,2+2
,2+2 ![]() ]
]
C.[0,4]
D.[﹣2﹣2 ![]() ,﹣2+2
,﹣2+2 ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|lg(x﹣1)|,若1<a<b且f(a)=f(b),则a+2b的取值范围为( )
A.![]()
B.![]()
C.(6,+∞)
D.[6,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的方程为(x﹣3)2+y2=1,圆M的方程为(x﹣3﹣3cosθ)2+(y﹣3sinθ)2=1(θ∈R),过M上任意一点P作圆C的两条切线PA,PB,切点分别为A、B,则∠APB的最大值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲抛掷均匀硬币2017次,乙抛掷均匀硬币2016次,下列四个随机事件的概率是0.5的是( )
①甲抛出正面次数比乙抛出正面次数多;
②甲抛出反面次数比乙抛出正面次数少;
③甲抛出反面次数比甲抛出正面次数多;
④乙抛出正面次数与乙抛出反面次数一样多.
A.①②
B.①③
C.②③
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,an+1=3an+1.
(1)证明{an+ ![]() }是等比数列,并求{an}的通项公式;
}是等比数列,并求{an}的通项公式;
(2)证明: ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com