
(09年东城区期末理)(14分)
如图,在直三棱柱![]() 中,
中,![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)在![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ∥平面
∥平面![]() ,若存在,试给出证明;若不存在,请说明理由.
,若存在,试给出证明;若不存在,请说明理由.

解析:解法一: (Ⅰ)在直三棱柱![]() 中,
中,![]() 底面
底面![]() ,
,![]() 在底面上的射影为
在底面上的射影为![]() .
.
由![]() 可得
可得![]() .
.
所以![]() . ………………..4分
. ………………..4分

(Ⅱ)过![]() 作
作![]() 于
于![]() ,连结
,连结![]() .
.
由![]() 底面
底面![]() 可得
可得![]() .
.
故![]() 为二面角
为二面角![]() 的平面角.
的平面角.
在![]() 中,
中,![]() ,
,
在Rt![]() 中,
中,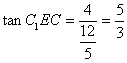 ,
,
故所求二面角的大小为![]() . ……………………………………9分
. ……………………………………9分
(Ⅲ)存在点![]() 使
使![]() ∥平面
∥平面![]() ,且
,且![]() 为
为![]() 中点,下面给出证明.
中点,下面给出证明.
设![]() 与
与![]() 交于点
交于点![]() 则
则![]() 为
为![]() 中点.
中点.
在![]() 中, 连结
中, 连结![]() ,
,![]() 分别为
分别为![]() 的中点,故
的中点,故![]() 为
为![]() 的中位线,
的中位线,
![]()
![]() ∥
∥![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]()
![]() ∥平面
∥平面![]() .
.
故存在点![]() 为
为![]() 中点,使
中点,使![]() ∥平面
∥平面![]() . ………………14分
. ………………14分
解法二 ![]() 直三棱柱
直三棱柱![]() ,底面三边长
,底面三边长![]() ,
,
![]() 两两垂直.
两两垂直.
如图以![]() 为坐标原点,建立空间直角坐标系
为坐标原点,建立空间直角坐标系![]() ,
,

则![]() .
.
(Ⅰ)![]() ,
,
![]() ,故
,故![]() . …………….4分
. …………….4分
(Ⅱ)平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
![]() ,
,![]() ,
,
由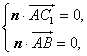 得
得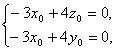
令![]() ,则
,则![]() .
.
则![]() .
.
故![]() <
<![]() >=
>=![]() .
.
所求二面角的大小为![]() . ……………………………………….9分
. ……………………………………….9分
(Ⅲ)同解法一 ……………………………………………………………..………..14分


科目:高中数学 来源: 题型:
(09年东城区期末理)(14分)
已知点![]() (
(![]() N
N![]() )顺次为直线
)顺次为直线![]() 上的点,点
上的点,点![]()
![]() (
(![]() N
N![]() )顺次为
)顺次为![]() 轴上的点,其中
轴上的点,其中![]() ,对任意的
,对任意的![]() N
N![]() ,点
,点![]() 、
、![]() 、
、![]() 构成以
构成以![]() 为顶点的等腰三角形.
为顶点的等腰三角形.
(Ⅰ)证明:数列![]() 是等差数列;
是等差数列;
(Ⅱ)求证:对任意的![]() N
N![]() ,
,![]() 是常数,并求数列
是常数,并求数列![]() 的通项公式;
的通项公式;
(Ⅲ)在上述等腰三角形![]() 中是否存在直角三角形,若存在,求出此时
中是否存在直角三角形,若存在,求出此时![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年东城区期末理)(13分)
北京的高考数学试卷中共有8道选择题,每个选择题都给了4个选项(其中有且仅有一个选项是正确的).评分标准规定:每题只选1项,答对得5分,不答或答错得0分.某考生每道题都给出了答案,已确定有4道题的答案是正确的,而其余的题中,有两道题每题都可判断其有两个选项是错误的,有一道题可以判断其一个选项是错误的,还有一道题因不理解题意只能乱猜.对于这8道选择题,试求:
(Ⅰ) 该考生得分为40分的概率;
(Ⅱ) 该考生所得分数![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com