
【题目】函数f(x)=Asin(ωx![]() )+1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为
)+1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为![]() .
.
(1)求函数f(x)的解析式;
(2)求函数y=f(x)的单调增区间;
(3)设α∈(0,![]() ),则f(
),则f(![]() )=2,求α的值.
)=2,求α的值.
【答案】(1)y=2sin(2x![]() )+1(2)函数f(x)的单调增区间:
)+1(2)函数f(x)的单调增区间:![]() k∈Z(3)α
k∈Z(3)α![]()
【解析】
(1)根据函数的最值求出![]() ,由相邻两条对称轴之间的距离为
,由相邻两条对称轴之间的距离为![]() ,确定函数的周期,进而求出
,确定函数的周期,进而求出![]() 值;
值;
(2)利用整体思想结合![]() 单调递增区间,即可求解;
单调递增区间,即可求解;
(3)由![]() ,求出关于
,求出关于![]() 的三角函数值,结合
的三角函数值,结合![]() 的范围,即可求出结论.
的范围,即可求出结论.
(1)∵函数f(x)的最大值为3,
∴A+1=3,即A=2.
∵函数图象的相邻两条对称轴之间的距离为![]() ,
,
∴最小正周期T=π,∴ω=2.
故函数f(x)的解析式为y=2sin(2x![]() )+1;
)+1;
(2)由![]() ,
,![]() ,
,
得![]() ,
,![]()
∴![]() ,
,![]() .
.
∴函数f(x)的单调增区间:![]() k∈Z;
k∈Z;
(3)∵f(![]() )=2sin(α
)=2sin(α![]() )+1=2,即sin(α
)+1=2,即sin(α![]() )
)![]() ,
,
∵0<α![]() ,∴
,∴![]() ,
,
∴α![]() ,故α
,故α![]() .
.


科目:高中数学 来源: 题型:
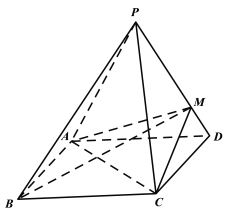
【题目】如图,四棱锥P-ABCD的底面是矩形,侧面PAD为等边三角形,AB=![]() ,AD=
,AD=![]() , PB=
, PB=![]() .
.
(1)求证:平面PAD⊥平面ABCD;
(2)M是棱PD上一点,三棱锥M-ABC的体积为1.记三棱锥P-MAC的体积为![]() ,三棱锥M-ACD的体积为
,三棱锥M-ACD的体积为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC三个内角A、B、C所对的边分别为![]() 已知
已知![]()
(1)求角B的大小;
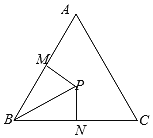
(2)如图,在△ABC内取一点P,使得PB=2,过点P分别作直线BA、BC的垂线PM、PN,垂足分别是M、N,设∠PBA=![]() 求四边形PMBN的面积的最大值及此时
求四边形PMBN的面积的最大值及此时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题为真命题的是( )
A.设命题![]() :
:![]() ,
,![]() .则
.则![]() :
:![]() ,
,![]() ;
;
B.若![]() ,
,![]() ,则
,则![]() ;
;
C.若![]() 是定义在
是定义在![]() 上的减函数,则“
上的减函数,则“![]() ”是“
”是“![]() ”的充要条件;
”的充要条件;
D.若![]() ,
,![]() ,
,![]() (
(![]() )是全不为0的实数,则“
)是全不为0的实数,则“![]() ”是“不等式
”是“不等式![]() 和
和![]() 解集相等”的充分不必要条件.
解集相等”的充分不必要条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】青岛二中有羽毛球社乒乓球社和篮球社,三个社团的人数分别为27,9,18,现采用分层抽样的方法从这三个社团中抽取6人参加活动.
(1)求应从这三个社团中分别抽取的学生人数;
(2)将抽取的6名学生进行编号,编号分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,从这6名学生中随机抽出2名参加体育测试.
,从这6名学生中随机抽出2名参加体育测试.
①用所给的编号列出所有可能的结果;
②设事件![]() 是“编号为
是“编号为![]() ,
,![]() 的两名学生至少有一人被抽到”,求事件
的两名学生至少有一人被抽到”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在实数集![]() 上的函数
上的函数![]() ,
,![]() 恒不为0,若存在不等于1的正常数
恒不为0,若存在不等于1的正常数![]() ,对于任意实数
,对于任意实数![]() ,等式
,等式![]() 恒成立,则称函数
恒成立,则称函数![]() 为
为![]() 函数.
函数.
(1)若函数![]() 为
为![]() 函数,求出
函数,求出![]() 的值;
的值;
(2)设![]() ,其中
,其中![]() 为自然对数的底数,函数
为自然对数的底数,函数![]() .
.
①比较![]() 与
与![]() 的大小;
的大小;
②判断函数![]() 是否为
是否为![]() 函数,若是,请证明;若不是,试说明理由.
函数,若是,请证明;若不是,试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学家欧拉在1765年提出定理:三角形的外心、重心、垂心依次位于同一直线上,且重心到外心的距离是重心到垂心距离的一半,这条直线被后人称之为三角形的欧拉线.已知△ABC的顶点A(2,0),B(0,4),且AC=BC,则△ABC的欧拉线的方程为( )
A.x+2y+3=0B.2x+y+3=0C.x﹣2y+3=0D.2x﹣y+3=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
在平面直角坐标系中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系.已知点A的极坐标(![]() ,
,![]() ),直线l的极坐标方程为ρcos(θ-
),直线l的极坐标方程为ρcos(θ-![]() )=a,.
)=a,.
(1)若点A在直线l上,求直线l的直角坐标方程;
(2)圆C的参数方程为![]() (
(![]() 为参数),若直线
为参数),若直线![]() 与圆C相交的弦长为
与圆C相交的弦长为![]() ,求
,求![]() 的值。
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com