(1)已知an是等差数列,其中a1=31,公差d=-8,则数列an前n项和的最大值为 .
(2)已知an是各项不为零的等差数列,其中a1>0,公差d<0,若S10=0,求数列an前 项和取得最大值.
【答案】
分析:(1)根据数列的首项和公差写出数列的前n项和,它是关于n的二次函数,二次项的系数小于零,函数存在最大值,结合二次函数的最值得到结果,注意变量n的取值.
(2)结合二次函数的图象,得到二次函数图象的开口向下,根据图象关于对称轴对称的特点,得到函数在对称轴处取到最大值,,注意对称轴对应的自变量应该是整数或离对称轴最近的整数.
解答:解:(1)∵a
n是等差数列,其中a
1=31,公差d=-8,
∴数列a
n前n项和s
n=-4n
2+35n,
根据二次函数的性质,当n=
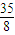
时,前n项和s
n取到最大值,
∵n∈N,
∴n=4,
∴前n项和s
n的最大值是s
n=-64+140=76,
(2)a
n是各项不为零的等差数列,
其中a
1>0,公差d<0,S
10=0,
根据二次函数的图象特点得到图象开口向下,且在n=
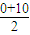
=5时,
数列a
n前5项和取得最大值.
点评:数列中数的有序性是数列定义的灵魂,要注意辨析数列中的项与数集中元素的异同,因此在研究数列问题时既要注意函数方法的普遍性,又要注意数列方法的特殊性.

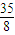 时,前n项和sn取到最大值,
时,前n项和sn取到最大值,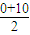 =5时,
=5时,

 阅读快车系列答案
阅读快车系列答案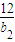 .
.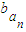 }是公比为9的等比数列,求证:
}是公比为9的等比数列,求证: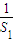 +
+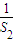 +…+
+…+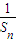 <
< .
.