
分析 由反射定律可得点A(-$\frac{1}{2}$,0)关于y轴的对称点A′($\frac{1}{2}$,0)在反射光线所在的直线上,再根据点B(0,1)也在反射光线所在的直线上,用两点式求得反射光线所在的直线方程.
解答 解:由反射定律可得点点A(-$\frac{1}{2}$,0)关于y轴的对称点A′($\frac{1}{2}$,0)在反射光线所在的直线上,
再根据点B(0,1)也在反射光线所在的直线上,
用两点式求得反射光线所在的直线方程为$\frac{y-1}{0-1}=\frac{x-0}{\frac{1}{2}-0}$,即2x+y-1=0,
故答案为:2x+y-1=0.
点评 本题主要考查求一个点关于直线的对称点的坐标,用两点式求直线的方程,属于基础题.


 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:解答题
 2016年1月1日,我国实施“全面二孩”政策,中国社会科学院在某地随机抽取了150名已婚男性,其中愿意生育二孩的有100名,经统计,该100名男性的年龄情况对应的频率分布直方图如下:
2016年1月1日,我国实施“全面二孩”政策,中国社会科学院在某地随机抽取了150名已婚男性,其中愿意生育二孩的有100名,经统计,该100名男性的年龄情况对应的频率分布直方图如下:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,$\frac{2}{3}$) | B. | [0,$\frac{3}{4}$) | C. | ($\frac{3}{4}$,+∞) | D. | (0,$\frac{2}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{1}{32}$ | B. | x=$\frac{1}{2}$ | C. | y=2 | D. | y=4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
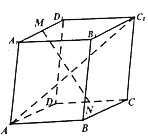 已知平行六面体ABCD-A1B1C1D1,设A1D1中点为M,CD的中点为N,若∠A1AD=∠A1AB=∠BAD=60°且AA1=AB=AD=1,则|AC1|=$\sqrt{6}$,若$\overrightarrow{MN}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$,则x+y+z=0.
已知平行六面体ABCD-A1B1C1D1,设A1D1中点为M,CD的中点为N,若∠A1AD=∠A1AB=∠BAD=60°且AA1=AB=AD=1,则|AC1|=$\sqrt{6}$,若$\overrightarrow{MN}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$,则x+y+z=0.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | ||
| C. | 2个 | D. | 不确定,随k的变化而变化 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com