
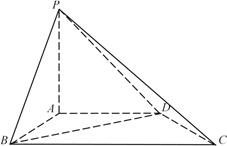
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥AD,AD∥BC,AP=AB=AD=1.
(Ⅰ)若直线PB与CD所成角的大小为![]() ,求BC的长;
,求BC的长;
(Ⅱ)求二面角B-PD-A的余弦值.
【答案】(1)2(2)![]()
【解析】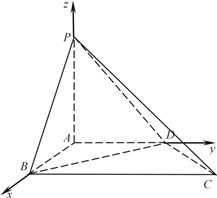
试题分析:(1)以![]() 为单位正交基底,建立空间直角坐标系
为单位正交基底,建立空间直角坐标系![]() .设
.设![]() ,则
,则![]() ,利用空间向量夹角余弦公式列方程求解即可;(2)分别求出平面PBD与平面PAD的一个法向量,根据空间向量夹角余弦公式,可得结果.
,利用空间向量夹角余弦公式列方程求解即可;(2)分别求出平面PBD与平面PAD的一个法向量,根据空间向量夹角余弦公式,可得结果.
试题解析:解:(1)以{![]() }为单位正交基底,建立如图所示的空间直角坐标系A-xyz.因为AP=AB=AD=1,所以A(0,0,0),B(1,0,0),D(0,1,0),P(0,0,1).设C(1,y,0),则
}为单位正交基底,建立如图所示的空间直角坐标系A-xyz.因为AP=AB=AD=1,所以A(0,0,0),B(1,0,0),D(0,1,0),P(0,0,1).设C(1,y,0),则![]() =(1,0,-1),
=(1,0,-1), ![]() =(-1,1-y,0). …………………2分
=(-1,1-y,0). …………………2分
因为直线PB与CD所成角大小为![]() ,
,
所以|cos<![]() ,
, ![]() >|=|
>|=| 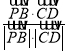 |=
|=![]() ,
,
即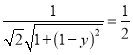 ,解得y=2或y=0(舍),
,解得y=2或y=0(舍),
所以C(1,2,0),所以BC的长为2.
(2)设平面PBD的一个法向量为n1=(x,y,z).
因为![]() =(1,0,-1),
=(1,0,-1), ![]() =(0,1,-1),
=(0,1,-1),
则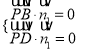 即
即![]()
令x=1,则y=1,z=1,所以n1=(1,1,1).
因为平面PAD的一个法向量为n2=(1,0,0),
所以cos<n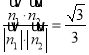
所以,由图可知二面角B-PD-A的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+bx(其中常数a,b∈R),g(x)=f(x)﹣f′(x)是奇函数,
(1)求f(x)的表达式;
(2)求g(x)在[1,3]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() (a>b>0)的右焦点F(1,0),离心率为
(a>b>0)的右焦点F(1,0),离心率为 ![]() ,过F作两条互相垂直的弦AB,CD,设AB,CD的中点分别为M,N.
,过F作两条互相垂直的弦AB,CD,设AB,CD的中点分别为M,N. 
(1)求椭圆的方程;
(2)证明:直线MN必过定点,并求出此定点坐标;
(3)若弦AB,CD的斜率均存在,求△FMN面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂有100名工人接受了生产1000台某产品的总任务,每台产品由9个甲型装置和3个乙型装置配套组成,每个工人每小时能加工完成1个甲型装置或3个乙型装置.现将工人分成两组分别加工甲型和乙型装置.设加工甲型装置的工人有x人,他们加工完甲型装置所需时间为t1小时,其余工人加工完乙型装置所需时间为t2小时.
设f(x)=t1+t2.
(Ⅰ)求f(x)的解析式,并写出其定义域;
(Ⅱ)当x等于多少时,f(x)取得最小值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知如图:平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点. 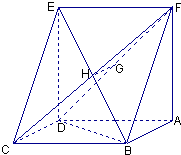
(1)求证:GH∥平面CDE;
(2)若CD=2,DB=4 ![]() ,求四棱锥F﹣ABCD的体积.
,求四棱锥F﹣ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=aln x+![]() (a>0).
(a>0).
(1)求函数f(x)的极值;
(2)若对任意的x>0,恒有ax(2-ln x)≤1,求实数a的取值范围;
(3)是否存在实数a,使得函数f(x)在[1,e]上的最小值为0?若存在,试求出a的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com