
【题目】【选修4-4:坐标系与参数方程】
在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系.已知曲线
轴的正半轴为极轴建立极坐标系.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .倾斜角为
.倾斜角为![]() ,且经过定点
,且经过定点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(Ⅰ)写出直线![]() 的参数方程的标准形式,并求曲线
的参数方程的标准形式,并求曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】已知圆O1和圆O2的极坐标方程分别为ρ=2,ρ2-2![]() ρcos(θ-
ρcos(θ-![]() )=2.
)=2.
(1)把圆O1和圆O2的极坐标方程化为直角坐标方程;
(2)设两圆交点分别为A、B,求直线AB的参数方程,并利用直线AB的参数方程求两圆的公共弦长|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() ),以椭圆内一点
),以椭圆内一点![]() 为中点作弦
为中点作弦![]() ,设线段
,设线段![]() 的中垂线与椭圆相交于
的中垂线与椭圆相交于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆的离心率;
(Ⅱ)试判断是否存在这样的![]() ,使得
,使得![]() ,
, ![]() ,
, ![]() ,
, ![]() 在同一个圆上,并说明理由.
在同一个圆上,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P—ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知BD=2AD=8,AB=2DC=4![]() .
.
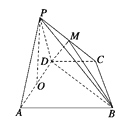
(1)设M是PC上的一点,求证:平面MBD⊥平面PAD;
(2)求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市理论预测2010年到2014年人口总数与年份的关系如下表所示
年份2010+x(年) | 0 | 1 | 2 | 3 | 4 |
人口数y(十万) | 5 | 7 | 8 | 11 | 19 |
(1)请根据上表提供的数据,求出y关于x的线性回归方程;
(2) 据此估计2015年该城市人口总数。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为减少空气污染,某市鼓励居民用电(减少燃气或燃煤),采用分段计费的方法计算:电费每月用电不超过100度时,按每度0.57元计算;每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分每度按0.5元计算.
(Ⅰ)设月用电![]() 度时,应交电费
度时,应交电费![]() 元,写出
元,写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(Ⅱ)小明家第一季度缴纳电费情况如下:
月份 | 一月 | 二月 | 三月 | 合计 |
交费金额 | 76元 | 63元 | 45.6元 | 184.6元 |
问小明家第一季度共用电多少度?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在甲、乙两个盒子中分别装有标号为1,2,3,4的四个球,现从甲乙两个盒子中各取出1个球,球的标号分别记做a,b,每个球被取出的可能性相等.
(1)求a+b能被3整除的概率;
(2)若|a-b|≤1则中奖,求中奖的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com