
【题目】设函数![]() ,
,![]() ,
,![]() ,
,
(1)求![]() 在
在![]() 处的切线的一般式方程;
处的切线的一般式方程;
(2)请判断![]() 与
与![]() 的图像有几个交点?
的图像有几个交点?
(3)设![]() 为函数
为函数![]() 的极值点,
的极值点,![]() 为
为![]() 与
与![]() 的图像一个交点的横坐标,且
的图像一个交点的横坐标,且![]() ,证明:
,证明:![]() .
.
【答案】(1)![]() (2)
(2)![]() 与
与![]() 的图像有2交点(3)证明见解析
的图像有2交点(3)证明见解析
【解析】
(1)利用导数求得切线的斜率,结合切点坐标求得切线方程.
(2)构造函数![]() ,利用导数研究
,利用导数研究![]() 的单调区间和零点,由此判断
的单调区间和零点,由此判断![]() 与
与![]() 的图像的交点个数.
的图像的交点个数.
(3)结合(2)以及题意得到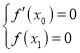 ,化简得到
,化简得到![]() ,利用放缩法以及取对数运算,化简证得
,利用放缩法以及取对数运算,化简证得![]() 成立.
成立.
(1)由![]() 得切线的斜率为
得切线的斜率为![]() ,切点为
,切点为![]() .
.
∴切线方程为:![]() ,
,
∴所求切线的一般式方程为![]() .
.
(2)令![]() 由题意可知,
由题意可知,![]() 的定义域为
的定义域为![]() ,
,
且![]() .
.
令![]() ,得
,得![]() ,由
,由![]() ,
,![]() 得,可知
得,可知![]() 在
在![]()
内单调递减,
又![]() ,且
,且![]() ,
,
故![]() 在
在![]() 内有唯一解,从而
内有唯一解,从而![]() 在
在![]() 内有唯一解,不妨设为
内有唯一解,不妨设为![]() ,
,
则![]() ,当
,当![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 内单调递增;
内单调递增;
当![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 内单调递减,
内单调递减,
因此![]() 是
是![]() 的唯一极值点.
的唯一极值点.
令![]() ,则当
,则当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 内单调递减,
内单调递减,
∴当![]() 时,
时,![]() ,即
,即![]() ,
,
从而![]()
![]() ,
,
又因为![]() ,∴
,∴![]() 在
在![]() 内有唯一零点,
内有唯一零点,
又![]() 在
在![]() 内有唯一零点1,从而,
内有唯一零点1,从而,![]() 在
在![]() 内恰有两个零点.
内恰有两个零点.
所以![]() 与
与![]() 的图像有2交点;
的图像有2交点;
(3)由(2)及题意,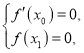 即
即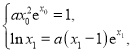
从而![]() ,即
,即![]() ,
,
∵当![]() 时,
时,![]() ,又
,又![]() ,故
,故![]() ,
,
两边取对数,得![]() ,
,
于是![]() ,整理得
,整理得![]() ,命题得证.
,命题得证.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
【题目】中国古代儒家要求学生掌握六种基本才艺:礼、乐、射、御、书、数,简称“六艺”,某高中学校为弘扬“六艺”的传统文化,分别进行了主题为“礼、乐、射、御、书、数”六场传统文化知识竞赛,现有甲、乙、丙三位选手进入了前三名的最后角逐,规定:每场知识竞赛前三名的得分都分别为![]()
![]() 且
且![]() ;选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为
;选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为![]() 分,乙和丙最后得分都是
分,乙和丙最后得分都是![]() 分,且乙在其中一场比赛中获得第一名,下列说法正确的是( )
分,且乙在其中一场比赛中获得第一名,下列说法正确的是( )
A. 乙有四场比赛获得第三名
B. 每场比赛第一名得分![]() 为
为![]()
C. 甲可能有一场比赛获得第二名
D. 丙可能有一场比赛获得第一名
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,准线方程为
,准线方程为![]() ,直线
,直线![]() 过定点
过定点![]() (
(![]() )且与抛物线交于
)且与抛物线交于![]() 、
、![]() 两点,
两点,![]() 为坐标原点.
为坐标原点.
(1)求抛物线的方程;
(2)![]() 是否为定值,若是,求出这个定值;若不是,请说明理由;
是否为定值,若是,求出这个定值;若不是,请说明理由;
(3)当![]() 时,设
时,设![]() ,记
,记![]() ,求
,求![]() 的解析式.
的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年诺贝尔生理学或医学奖获得者威廉·凯林(WilliamG.KaelinJr)在研究肾癌的
年诺贝尔生理学或医学奖获得者威廉·凯林(WilliamG.KaelinJr)在研究肾癌的![]() 抑制剂过程中使用的输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下液体(滴管内液体忽略不计),设输液开始后
抑制剂过程中使用的输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下液体(滴管内液体忽略不计),设输液开始后![]() 分钟,瓶内液面与进气管的距离为
分钟,瓶内液面与进气管的距离为![]() 厘米,已知当
厘米,已知当![]() 时,
时,![]() .如果瓶内的药液恰好
.如果瓶内的药液恰好![]() 分钟滴完.则函数
分钟滴完.则函数![]() 的图像为( )
的图像为( )

A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国古代数学家刘徽用圆内接正多边形的面积去逼近圆的面积求圆周率![]() ,他从单位圆内接正六边形算起,令边数一倍一倍地增加,即12,24,48,…,192,…,逐个算出正六边形,正十二边形,正二十四边形,…,正一百九十二边形,…的面积,这些数值逐步地逼近圆面积,刘徽算到了正一百九十二边形,这时候
,他从单位圆内接正六边形算起,令边数一倍一倍地增加,即12,24,48,…,192,…,逐个算出正六边形,正十二边形,正二十四边形,…,正一百九十二边形,…的面积,这些数值逐步地逼近圆面积,刘徽算到了正一百九十二边形,这时候![]() 的近似值是3.141024,刘徽称这个方法为“割圆术”,并且把“割圆术”的特点概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”.刘徽这种想法的可贵之处在于用已知的、可求的来逼近未知的、要求的,用有限来逼近无穷,这种思想极其重要,对后世产生了巨大影响.按照上面“割圆术”,用正二十四边形来估算圆周率,则
的近似值是3.141024,刘徽称这个方法为“割圆术”,并且把“割圆术”的特点概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”.刘徽这种想法的可贵之处在于用已知的、可求的来逼近未知的、要求的,用有限来逼近无穷,这种思想极其重要,对后世产生了巨大影响.按照上面“割圆术”,用正二十四边形来估算圆周率,则![]() 的近似值是( )(精确到
的近似值是( )(精确到![]() ).(参考数据
).(参考数据![]() )
)
A.3.14B.3.11C.3.10D.3.05
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农科所对冬季昼夜温差(最高温度与最低温度的差)大小与某反季节大豆新品种一天内发芽数之间的关系进行了分析研究,他们分别记录了12月1日至12月6日每天昼夜最高、最低的温度(如图甲),以及实验室每天每100颗种子中的发芽数情况(如图乙),得到如下资料:
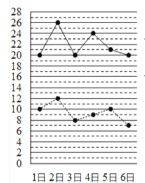
![]() 最高温度
最高温度![]() 最低温度
最低温度
甲
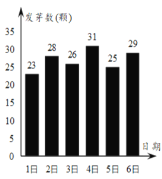
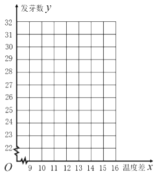
乙
(1)请画出发芽数y与温差x的散点图;
(2)若建立发芽数y与温差x之间的线性回归模型,请用相关系数说明建立模型的合理性;
(3)①求出发芽数y与温差x之间的回归方程![]() (系数精确到0.01);
(系数精确到0.01);
②若12月7日的昼夜温差为![]() ,通过建立的y关于x的回归方程,估计该实验室12月7日当天100颗种子的发芽数.
,通过建立的y关于x的回归方程,估计该实验室12月7日当天100颗种子的发芽数.
参考数据:![]()
![]()
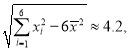
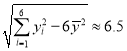 .
.
参考公式:
相关系数: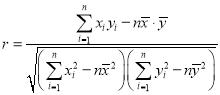 (当
(当![]() 时,具有较强的相关关系).
时,具有较强的相关关系).
回归方程![]() 中斜率和截距计算公式:
中斜率和截距计算公式:
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ,
,![]() ,②
,②![]() ,
,![]() ,③
,③![]() ,
,![]() 三个条件中任选一个补充在下面问题中,并加以解答.
三个条件中任选一个补充在下面问题中,并加以解答.
已知![]() 的内角A,B,C的对边分别为a,b,c,若
的内角A,B,C的对边分别为a,b,c,若![]() ,______,求
,______,求![]() 的面积S.
的面积S.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]()
![]() 为公海与领海的分界线,一艘巡逻艇在原点
为公海与领海的分界线,一艘巡逻艇在原点![]() 处发现了北偏东
处发现了北偏东![]() 海面上
海面上![]() 处有一艘走私船,走私船正向停泊在公海上接应的走私海轮
处有一艘走私船,走私船正向停泊在公海上接应的走私海轮![]() 航行,以便上海轮后逃窜.已知巡逻艇的航速是走私船航速的2倍,且两者都是沿直线航行,但走私船可能向任一方向逃窜.
航行,以便上海轮后逃窜.已知巡逻艇的航速是走私船航速的2倍,且两者都是沿直线航行,但走私船可能向任一方向逃窜.
(1)如果走私船和巡逻船相距6海里,求走私船能被截获的点的轨迹;
(2)若![]() 与公海的最近距离20海里,要保证在领海内捕获走私船,则
与公海的最近距离20海里,要保证在领海内捕获走私船,则![]() ,
,![]() 之间的最远距离是多少海里?
之间的最远距离是多少海里?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com