
【题目】已知函数f(x)=x2+ax(a>0)在[﹣1,2]上的最大值为8,函数g(x)是h(x)=ex的反函数.
(1)求函数g(f(x))的单调区间;
(2)求证:函数y=f(x)h(x)﹣ ![]() (x>0)恰有一个零点x0 , 且g(x0)<x02h(x0)﹣1 (参考数据:e=2.71828…,ln2≈0.693).
(x>0)恰有一个零点x0 , 且g(x0)<x02h(x0)﹣1 (参考数据:e=2.71828…,ln2≈0.693).
【答案】
(1)解:函数g(x)是h(x)=ex的反函数,
可得g(x)=lnx;
函数f(x)=x2+ax(a>0)在[﹣1,2]上的最大值为8,
只能是f(﹣1)=8或f(2)=8,
即有1﹣a=8或4+2a=8,
解得a=2(﹣7舍去),
函数g(f(x))=ln(x2+2x),
由x2+2x>0,可得x>0或x<﹣2.
由复合函数的单调性,可得
函数g(f(x))的单调增区间为(0,+∞);
单调减区间为(﹣∞,﹣2);
(2)证明:由(1)得:f(x)=x2+2x,即φ(x)=f(x)h(x)﹣ ![]() ,(x>0),
,(x>0),
设0<x1<x2,则x1﹣x2<0,x1x2>0,∴ ![]() <0,
<0,
∵f(x)在(0,+∞)递增且f(x)>0,
∴f(x2)>f(x1)>0,
∵ ![]() >
> ![]() >0,∴f(x1)
>0,∴f(x1) ![]() <f(x2)
<f(x2) ![]() ,
,
∴φ(x1)﹣φ(x2)=f(x1) ![]() ﹣f(x2)
﹣f(x2) ![]() +
+ ![]() <0,
<0,
即φ(x1)<φ(x2),∴φ(x)在(0,+∞)递增;
∵φ( ![]() )=
)= ![]() ﹣2>
﹣2> ![]() ﹣2=0,
﹣2=0,
φ( ![]() )=
)= ![]() ﹣e<
﹣e< ![]() ﹣e<0,
﹣e<0,
即φ( ![]() )φ(
)φ( ![]() )<0,
)<0,
∴函数y=f(x)h(x)﹣ ![]() (x>0)恰有1个零点x0,且x0∈(
(x>0)恰有1个零点x0,且x0∈( ![]() ,
, ![]() ),
),
∴( ![]() +2x0)
+2x0) ![]() ﹣
﹣ ![]() =0,即
=0,即 ![]() =
= ![]() ,
,
∴ ![]() h(x0)﹣g(x0)=
h(x0)﹣g(x0)= ![]() ﹣lnx0=
﹣lnx0= ![]() ﹣lnx0,
﹣lnx0,
∵y= ![]() ﹣lnx在(0,
﹣lnx在(0, ![]() )上是减函数,
)上是减函数,
∴ ![]() ﹣lnx0>
﹣lnx0> ![]() ﹣ln
﹣ln ![]() =
= ![]() +ln2>
+ln2> ![]() +0.6=1,
+0.6=1,
即g(x0)< ![]() h(x0)﹣1,
h(x0)﹣1,
综上,函数y=f(x)h(x)﹣ ![]() (x>0)恰有一个零点x0,且g(x0)<x02h(x0)﹣1.
(x>0)恰有一个零点x0,且g(x0)<x02h(x0)﹣1.
【解析】(1)求出g(x)的解析式以及a的值,从而求出g(f(x))的解析式,求出函数 的单调区间即可;(2)令φ(x)=f(x)h(x)﹣ ![]() ,(x>0),根据函数的单调性得到φ(x)在(0,+∞)递增;从而证出结论.
,(x>0),根据函数的单调性得到φ(x)在(0,+∞)递增;从而证出结论.
【考点精析】关于本题考查的利用导数研究函数的单调性和函数的最大(小)值与导数,需要了解一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能得出正确答案.
比较,其中最大的是一个最大值,最小的是最小值才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】设命题p:实数x满足x2﹣4ax+3a2<0(a>0),命题q:实数x满足 ![]() ≤0。
≤0。
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若¬p是¬q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,AB=AD=1,BC=2,又PB⊥平面ABCD,且PB=1,点E在棱PD上,且DE=2PE.
(Ⅰ)求异面直线PA与CD所成的角的大小;
(Ⅱ)求证:BE⊥平面PCD;
(Ⅲ)求二面角A﹣PD﹣B的大小.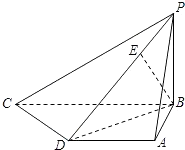
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】元代数学家朱世杰所著《四元玉鉴》一书,是中国古代数学的重要著作之一,共分卷首、上卷、中卷、下卷四卷,下卷中《果垛叠藏》第一问是:“今有三角垛果子一所,值钱一贯三百二十文,只云从上一个值钱二文,次下层层每个累贯一文,问底子每面几何?”据此,绘制如图所示程序框图,求得底面每边的果子数n为( ) 
A.7
B.8
C.9
D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:实数x满足x2﹣4ax+3a2<0,其中a>0,命题q:实数x满足 ![]() . (Ⅰ)若a=1,且p∧q为真,求实数x的取值范围;
. (Ⅰ)若a=1,且p∧q为真,求实数x的取值范围;
(Ⅱ)若¬p是¬q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知直线2x﹣y﹣4=0与直线x﹣2y+1=0交于点p.
(1)求过点p且垂直于直线3x+4y﹣15=0的直线l1的方程;(结果写成直线方程的一般式)
(2)求过点P并且在两坐标轴上截距相等的直线l2方程(结果写成直线方程的一般式)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于实数x的不等式﹣x2+bx+c<0的解集是{x|x<﹣3或x>2},则关于x的不等式cx2﹣bx﹣1>0的解集是( )
A.(﹣ ![]() ,
, ![]() )
)
B.(﹣2,3)
C.(﹣∞,﹣ ![]() )∪(
)∪( ![]() ,+∞)
,+∞)
D.(﹣∞,﹣2)∪(3,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com