
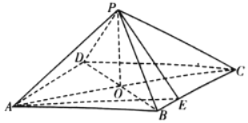
【题目】如图,四棱锥![]() 中,四边形
中,四边形![]() 是菱形,
是菱形,![]() ,
,![]() ,E是
,E是![]() 上一点,且
上一点,且![]() ,设
,设![]() .
.
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)由已知可得![]() ,
,![]() ,由直线与平面垂直的判定可得
,由直线与平面垂直的判定可得![]() 平面
平面![]() ,得到
,得到![]() ,再由
,再由![]() ,进一步得到
,进一步得到![]() 平面
平面![]() ;
;
(2)由(1)知,![]() 平面
平面![]() ,
,![]() ,以O为坐标原点,分别以
,以O为坐标原点,分别以![]() ,
,![]() ,
,![]() 所在直线为x,y,z轴建立空间直角坐标系,设四边形
所在直线为x,y,z轴建立空间直角坐标系,设四边形![]() 的边长为4,
的边长为4,![]() ,由
,由![]() 列式求解a,可得所用点的坐标,再求出平面
列式求解a,可得所用点的坐标,再求出平面![]() 与平面
与平面![]() 的一个法向量,由两法向量所成角的余弦值可得二面角
的一个法向量,由两法向量所成角的余弦值可得二面角![]() 的余弦值.
的余弦值.
(1)证明:∵四边形![]() 是菱形,∴O是
是菱形,∴O是![]() 的中点,
的中点,![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
∵![]() ,O是
,O是![]() 的中点,∴
的中点,∴![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ;
;

(2)解:由(1)知,![]() 平面
平面![]() ,
,![]() .
.
∴以O为坐标原点,以![]() ,
,![]() ,
,![]() 所在直线为x,y,z轴建立空间直角坐标系.
所在直线为x,y,z轴建立空间直角坐标系.
设四边形![]() 的边长为4,
的边长为4,![]() .
.
∵四边形![]() 是菱形,
是菱形,![]() ,∴
,∴![]() 与
与![]() 都是等边三角形.
都是等边三角形.
∴![]() .
.
∴![]() ,
,![]() ,
,![]() ,
, ,
,
![]() ,
, ,
, .
.
∵![]() ,∴
,∴ ,
,
即![]() ,得
,得![]() .
.
∴![]() ,
, .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
由 ,取
,取![]() ,得
,得 ;
;
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由 ,取
,取![]() ,得
,得![]() .
.
设二面角![]() 的平面角为
的平面角为![]() ,由图可得,
,由图可得,![]() 为钝角,
为钝角,
则 .
.
∴二面角![]() 的余弦值为
的余弦值为![]() .
.


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:
【题目】假定某射手每次射击命中的概率为![]() ,且只有3发子弹.该射手一旦射中目标,就停止射击,否则就一直独立地射击到子弹用完.设耗用子弹数为X,求:
,且只有3发子弹.该射手一旦射中目标,就停止射击,否则就一直独立地射击到子弹用完.设耗用子弹数为X,求:
(1)目标被击中的概率;
(2)X的概率分布列;
(3)均值![]() ,方差V(X).
,方差V(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三国时代吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明,下面是赵爽的弦图及注文,弦图是一个以勾股形之弦为边的正方形,其面积称为弦实,图中包含四个全等的勾股形及一个小正方形,分别涂成红(朱)色及黄色其面积称为朱实,黄实,利朱用2×勾×股+(股-勾)2=4×朱实+黄实=弦实,化简得勾2+股2=弦2,设勾股中勾股比为![]() ,若向弦图内随机抛掷1000颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )
,若向弦图内随机抛掷1000颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )
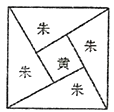
A.886B.500C.300D.134
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是椭圆T.
是椭圆T.![]() 上的两点,且A点位于第一象限.过A做x轴的垂线,垂足为点C,点D满足
上的两点,且A点位于第一象限.过A做x轴的垂线,垂足为点C,点D满足![]() ,延长
,延长![]() 交T于点
交T于点![]() .
.
(1)设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() .
.
(i)求证:![]() ;
;
(ii)证明:![]() 是直角三角形;
是直角三角形;
(2)求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周髀算经》是我国古老的天文学和数学著作,其书中记载:一年有二十四个节气,每个节气晷长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测影子的长度),夏至、小暑、大暑、立秋、处暑、白露、秋分、寒露、霜降是连续的九个节气,其晷长依次成等差数列,经记录测算,这九个节气的所有晷长之和为49.5尺,夏至、大暑、处暑三个节气晷长之和为10.5尺,则立秋的晷长为( )
A.1.5尺B.2.5尺C.3.5尺D.4.5尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学有初中学生1800人,高中学生1200人,为了解学生本学期课外阅读时间,现采用分成抽样的方法,从中抽取了100名学生,先统计了他们课外阅读时间,然后按“初中学生”和“高中学生”分为两组,再将每组学生的阅读时间(单位:小时)分为5组:[0,10),[10,20),[20,30),[30,40),[40,50],并分别加以统计,得到如图所示的频率分布直方图.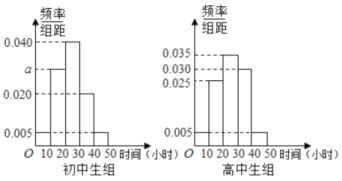
(1)写出![]() 的值;试估计该校所有学生中,阅读时间不小于30个小时的学生人数;
的值;试估计该校所有学生中,阅读时间不小于30个小时的学生人数;
(2)从阅读时间不足10个小时的样本学生中随机抽取3人,并用![]() 表示其中初中生的人数,求
表示其中初中生的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,侧面
中,侧面![]()
![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() 的中点.
的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在求出
,若存在求出![]() 的长,若不存在说明理由.
的长,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业引进现代化管理体制,生产效益明显提高,2019年全年总收入与2018年全年总收入相比增长了一倍,同时该企业的各项运营成本也随着收入的变化发生相应变化,下图给出了该企业这两年不同运营成本占全年总收入的比例,下列说法错误的是( )
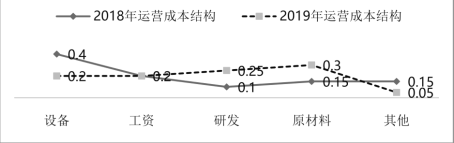
A.该企业2019年研发的费用与原材料的费用超过当年总收入的50%
B.该企业2019年设备支出金额及原材料的费用均与2018相当
C.该企业2019年工资支出总额比2018年多一倍
D.该企业2018年与2019研发的总费用占这两年总收入的20%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com