
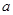 为非负实数,函数
为非负实数,函数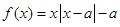 .
. 时,求函数的单调区间;
时,求函数的单调区间; 的零点个数.
的零点个数.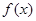 的单调递增区间是
的单调递增区间是 和
和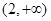 ,单调递减区间是
,单调递减区间是 .
. 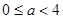 时,函数有一个零点;
时,函数有一个零点;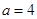 时,函数有两个零点;
时,函数有两个零点; 时,函数有三个零点.
时,函数有三个零点.  时,
时, ,然后对于分段函数各段的情况分别说明单调性,整体来合并得到结论。
,然后对于分段函数各段的情况分别说明单调性,整体来合并得到结论。 时,
时,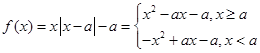 ,
, 时,
时, ,二次函数对称轴
,二次函数对称轴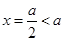 ,那么结合二次函数的 性质可知顶点的函数值为正数,负数,还是零,来确定零点的问题。
,那么结合二次函数的 性质可知顶点的函数值为正数,负数,还是零,来确定零点的问题。 时,
时, ,
, 时,
时,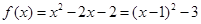 ,∴
,∴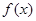 在
在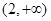 上单调递增;
上单调递增; 时,
时, ,
,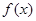 在
在 上单调递减,在
上单调递减,在 上单调递增;
上单调递增;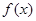 的单调递增区间是
的单调递增区间是 和
和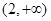 ,单调递减区间是
,单调递减区间是 .
. 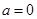 时,
时, ,函数
,函数 的零点为
的零点为 ;
;  时,
时,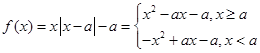 ,
, 时,
时, ,二次函数对称轴
,二次函数对称轴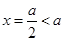 ,
,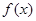 在
在 上单调递增,又
上单调递增,又 ,f(x)与x轴在
,f(x)与x轴在 有唯一交点;
有唯一交点;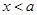 时,
时, ,二次函数对称轴
,二次函数对称轴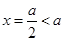 ,
,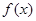 在
在 上单调递减,在
上单调递减,在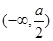 上单调递增;∴
上单调递增;∴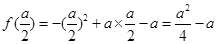 ,
, 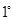 当
当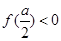 ,即
,即 时,函数
时,函数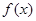 与
与 轴只有唯一交点,即唯一零点,
轴只有唯一交点,即唯一零点, 当
当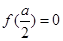 ,即
,即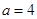 时,函数
时,函数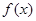 与
与 轴有两个交点,即两个零点
轴有两个交点,即两个零点 当
当 ,即
,即 时,f(a)<0,函数
时,f(a)<0,函数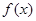 与
与 轴有三个交点,即有三个零点
轴有三个交点,即有三个零点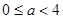 时,函数有一个零点;
时,函数有一个零点;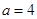 时,函数有两个零点;
时,函数有两个零点; 时,函数有三个零点.
时,函数有三个零点. 

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
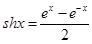 和双曲余弦函数
和双曲余弦函数 ,双曲正弦函数和双曲余弦函数与我们学过的正弦函数和余弦函数有许多相类似的性质,请类比正、余弦函数的和角或差角公式,写出关于双曲正弦、双曲余弦函数的一个正确的类似公式 。
,双曲正弦函数和双曲余弦函数与我们学过的正弦函数和余弦函数有许多相类似的性质,请类比正、余弦函数的和角或差角公式,写出关于双曲正弦、双曲余弦函数的一个正确的类似公式 。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
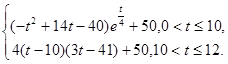
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
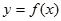 ,若同时满足下列条件:①
,若同时满足下列条件:①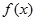 在D内单调递增或单调递减;②存在区间[
在D内单调递增或单调递减;②存在区间[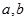 ]
]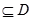 ,使
,使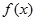 在[
在[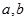 ]上的值域为[
]上的值域为[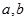 ];那么把
];那么把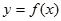 (
( )叫闭函数.
)叫闭函数.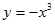 符合条件②的区间[
符合条件②的区间[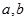 ];
];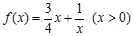 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;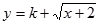 是闭函数,求实数
是闭函数,求实数 的取值范围.
的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com