
【题目】已知函数f(x)= ![]() sin
sin ![]() cos
cos ![]() +sin2
+sin2 ![]() (ω>0,0<φ<
(ω>0,0<φ< ![]() ).其图象的两个相邻对称中心的距离为
).其图象的两个相邻对称中心的距离为 ![]() ,且过点(
,且过点( ![]() ,1).
,1).
(1)函数f(x)的解析式;
(2)在△ABC中,角A,B,C所对的边分别为a,b,c.已知 ![]() =
= ![]() .且f(A)=
.且f(A)= ![]() ,求角C的大小.
,求角C的大小.
【答案】
(1)解:由题意得,f(x)= ![]() sin(ωx+φ)+
sin(ωx+φ)+ ![]() [1﹣cos(ωx+φ)]
[1﹣cos(ωx+φ)]
= ![]() ,
,
∵两个相邻对称中心的距离为 ![]() ,则T=π,
,则T=π,
∴ ![]() ,且ω>0,解得ω=2,
,且ω>0,解得ω=2,
又f(x)过点 ![]() ,∴
,∴ ![]() ,
,
则 ![]() ,即cosφ=
,即cosφ= ![]() ,由0<φ<
,由0<φ< ![]() 得,φ=
得,φ= ![]() ,
,
∴f(x)= ![]() ;
;
(2)解:在△ABC中,由余弦定理得b2=a2+c2﹣2accosB,
∴b2﹣a2﹣c2=﹣2accosB,
同理可得,c2﹣a2﹣b2=﹣2abcosC,
代入 ![]() 得,
得, ![]() =
= ![]() ,
,
由正弦定理得, ![]() ,
,
由0<C<π得sinC≠0,∴sinBcosC=2sinAcosB﹣sinCcosB,
∴2sinAcosB=sinBcosC+sinCcosB=sin(B+C)=sinA,
由0<A<π得sinA≠0,化简得cosB= ![]() ,
,
∵0<B<π,∴B= ![]() ,
,
由 ![]() 得
得 ![]() ,则
,则 ![]() ,
,
∵ ![]() ,∴
,∴ ![]() ,则
,则 ![]() 或
或 ![]() ,
,
解得 ![]() 或
或 ![]() ,
,
所以当 ![]() 时,
时, ![]() ;当
;当 ![]() 时,
时, ![]()
【解析】(1)根据二倍角公式、两角差的正弦公式化简解析式,结合条件求出周期,由周期公式求出ω,将点 ![]() 代入解析式化简后,由内角的范围和特殊角的三角函数值求出φ,即可求出f(x);(2)由正弦定理和余弦定理化简已知的式子,利用两角和的正弦公式和内角的范围求出B,由解析式化简
代入解析式化简后,由内角的范围和特殊角的三角函数值求出φ,即可求出f(x);(2)由正弦定理和余弦定理化简已知的式子,利用两角和的正弦公式和内角的范围求出B,由解析式化简 ![]() ,根据角A的范围和特殊角的三角函数值求出A,再由内角和定理求出C.
,根据角A的范围和特殊角的三角函数值求出A,再由内角和定理求出C.
【考点精析】根据题目的已知条件,利用正弦定理的定义的相关知识可以得到问题的答案,需要掌握正弦定理:![]() .
.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S ABCD中,平面SAD⊥平面ABCD.四边形ABCD为正方形,且点P为AD的中点,点Q为SB的中点.

(1)求证:CD⊥平面SAD.
(2)求证:PQ∥平面SCD.
(3)若SA=SD,点M为BC的中点,在棱SC上是否存在点N,使得平面DMN⊥平面ABCD?若存在,请说明其位置,并加以证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1,F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为1的直角三角形.
(1)求该椭圆的离心率和标准方程;
(2)点M为该椭圆上任意一点,求|MA|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了鼓励市民节约用水,实行“阶梯式”水价,将该市每户居民的月用水量划分为三档:月用水量不超过4吨的部分按2元/吨收费,超过4吨但不超过8吨的部分按4元/吨收费,超过8吨的部分按8元/吨收费.
(1)求居民月用水量费用![]() (单位:元)关于月用电量
(单位:元)关于月用电量![]() (单位:吨)的函数解析式;
(单位:吨)的函数解析式;
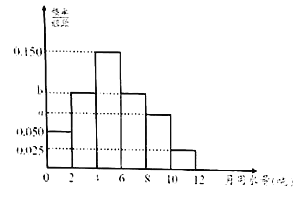
(2)为了了解居民的用水情况,通过抽样,获得今年3月份100户居民每户的用水量,统计分析后得到如图所示的频率分布直方图,若这100户居民中,今年3月份用水费用不超过16元的占66%,求![]() 的值;
的值;
(3)在满足条件(2)的条件下,若以这100户居民用水量的频率代替该月全市居民用户用水量的概率.且同组中的数据用该组区间的中点值代替.记为该市居民用户3月份的用水费用,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正三角形![]() 所在平面与梯形
所在平面与梯形![]() 所在平面垂直,
所在平面垂直, ![]() ,
, ![]() ,
, ![]() 为棱
为棱![]() 的中点.
的中点.
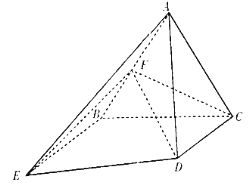
(1)求证: ![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成的角为30°,求三棱锥
所成的角为30°,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(1,
=(1, ![]() ),
), ![]() =(sinx,cosx),设函数f(x)=
=(sinx,cosx),设函数f(x)= ![]()
![]()
(1)求函数f(x)的最小正周期和最大值;
(2)设锐角△ABC的三个内角A,B,C的对边分别为a,b,c,若c= ![]() ,cosB=
,cosB= ![]() ,且f(C)=
,且f(C)= ![]() ,求b.
,求b.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产产品过程中记录的产量x(吨)与相应的生产能耗y(吨)标准煤的几组对照数据:
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)求y关于x的线性回归方程;(已知 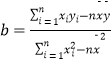 )
)
(2)已知该厂技术改造前100吨甲产品能耗为90吨标准煤,试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低了多少吨标准煤.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com