
【题目】2019年,河北等8省公布了高考改革综合方案将采取“3+1+2”模式,即语文、数学、英语必考,然后考生先在物理、历史中选择1门,再在思想政治、地理、化学、生物中选择2门.为了更好进行生涯规划,甲同学对高一一年来的七次考试成绩进行统计分析,其中物理、历史成绩的茎叶图如图所示.

(1)若甲同学随机选择3门功课,求他选到物理、地理两门功课的概率;
(2)试根据茎叶图分析甲同学应在物理和历史中选择哪一门学科?并说明理由;
(3)甲同学发现,其物理考试成绩![]() (分)与班级平均分
(分)与班级平均分![]() (分)具有线性相关关系,统计数据如下表所示,试求当班级平均分为50分时,其物理考试成绩.
(分)具有线性相关关系,统计数据如下表所示,试求当班级平均分为50分时,其物理考试成绩.

参考数据: ![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式:![]() ,
,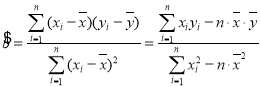 ,
,![]() (计算
(计算![]() 时精确到
时精确到![]() ).
).
【答案】(1)![]() ;(2)见解析;(3)见解析
;(2)见解析;(3)见解析
【解析】
(1)列出基本事件的所有情况,然后再列出满足条件的所有情况,利用古典概率公式即可得到答案.
(2)计算平均值和方差,从而比较甲同学应在物理和历史中选择哪一门学科;
(3)先计算![]() 和
和![]() ,然后通过公式计算出线性回归方程,然后代入平均值50即可得到答案.
,然后通过公式计算出线性回归方程,然后代入平均值50即可得到答案.
(1)记物理、历史分别为![]() ,思想政治、地理、化学、生物分别为
,思想政治、地理、化学、生物分别为![]() ,
,
由题意可知考生选择的情形有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共12种
,共12种
他选到物理、地理两门功课的满情形有![]() ,共3种
,共3种
![]() 甲同学选到物理、地理两门功课的概率为
甲同学选到物理、地理两门功课的概率为![]()
(2)物理成绩的平均分为![]()
历史成绩的平均分为![]()
由茎叶图可知物理成绩的方差![]() 历史成绩的方差
历史成绩的方差![]()
故从平均分来看,选择物理历史学科均可以;从方差的稳定性来看,应选择物理学科;从最高分的情况来看,应选择历史学科(答对一点即可)
(3)![]() ,
,![]() ,
,

![]()
![]() 关于
关于![]() 的回归方程为
的回归方程为![]()
当![]() 时,
时,![]() ,当班级平均分为50分时,其物理考试成绩为73分
,当班级平均分为50分时,其物理考试成绩为73分


科目:高中数学 来源: 题型:
【题目】(1)设直线![]() 的方程为
的方程为![]() .若直线
.若直线![]() 在两坐标轴上的截距相等,求直线
在两坐标轴上的截距相等,求直线![]() 的方程;
的方程;
(2)过直线![]() :
:![]() 上的点
上的点![]() 作直线
作直线![]() ,若直线
,若直线![]() ,
,![]() 与
与![]() 轴围成的三角形的面积为2,则直线
轴围成的三角形的面积为2,则直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的三个顶点
的三个顶点![]() ,其外接圆为圆
,其外接圆为圆![]() .
.
(1)若直线![]() 过点
过点![]() ,且被圆
,且被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)对于线段![]() (包括端点)上的任意一点
(包括端点)上的任意一点![]() ,若在以
,若在以![]() 为圆心的圆上都存在不同的两点
为圆心的圆上都存在不同的两点![]() ,使得点
,使得点![]() 是线段
是线段![]() 的中点,求圆
的中点,求圆![]() 的半径
的半径![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一某班的一次数学测试成绩的茎叶图和频率分布直方图因故都受到不同程度的损坏,但可见部分如下,据此解答如下问题: 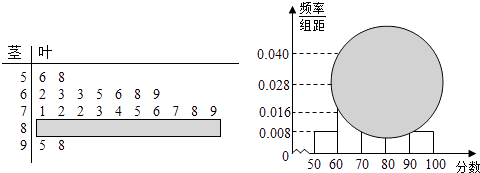
(Ⅰ)求分数在[50,60)的频率及全班人数;
(Ⅱ)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(Ⅲ)若规定:75(包含75分)分以上为良好,90分(包含90分)以上为优秀,要从分数在良好以上的试卷中任取两份分析学生失分情况,设在抽取的试卷中,分数为优秀的试卷份数为X,求X的概率分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l经过点A(﹣1,0),其倾斜角是α,以原点O为极点,以x轴的非负半轴为极轴,与直角坐标系xOy取相同的长度单位,建立极坐标系.设曲线C的极坐标方程是ρ2=6ρcosθ﹣5.
(Ⅰ)若直线l和曲线C有公共点,求倾斜角α的取值范围;
(Ⅱ)设B(x,y)为曲线C任意一点,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某市高三教学质量检测中,全市共有![]() 名学生参加了本次考试,其中示范性高中参加考试学生人数为
名学生参加了本次考试,其中示范性高中参加考试学生人数为![]() 人,非示范性高中参加考试学生人数为
人,非示范性高中参加考试学生人数为![]() 人.现从所有参加考试的学生中随机抽取
人.现从所有参加考试的学生中随机抽取![]() 人,作检测成绩数据分析.
人,作检测成绩数据分析.

(1)设计合理的抽样方案(说明抽样方法和样本构成即可);
(2)依据![]() 人的数学成绩绘制了如图所示的频率分布直方图,据此估计本次检测全市学生数学成绩的平均分;
人的数学成绩绘制了如图所示的频率分布直方图,据此估计本次检测全市学生数学成绩的平均分;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线C:x2=4y的焦点为F,斜率为k的直线l经过点F,若抛物线C上存在四个点到直线l的距离为2,则k的取值范围是( )
A.(﹣∞,﹣ ![]() )∪(
)∪( ![]() ,+∞)
,+∞)
B.(﹣ ![]() ,﹣1)∪(1,
,﹣1)∪(1, ![]() )
)
C.(﹣ ![]() ,
, ![]() )
)
D.(﹣∞,﹣1)∪(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PA⊥平面ABCD,四边形ABCD为梯形,AD∥BC,BC=6,PA=AD=CD=2,E为BC上一点且BE= ![]() BC,PB⊥AE.
BC,PB⊥AE. 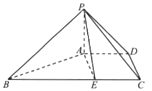
(1)求证:AB⊥PE;
(2)求二面角B﹣PC﹣D的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com