Question

(本小题满10分) 设直线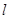的方程为．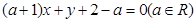

(1) 若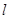在两坐标轴上的截距相等，求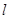的方程；

(2) 若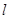不经过第二象限，求实数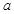的取值范围．

 

Answer 1

【答案】

 (1) 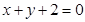.(2) a≤－1.

【解析】

试题分析：

（Ⅰ）根据直线方程求出它在两坐标轴上的截距，根据它在两坐标轴上的截距相等，求出a的值，即得直线l方程．

（Ⅱ）把直线方程化为斜截式为 y=-（a+1）x-a-2，若l不经过第二象限，则a=-1 或 -(a+1)》0，-a-2≤0，由此求得实数a的取值范围。

解：(1)当直线过原点时，该直线在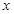轴和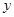轴上的截距都为零，截距相等，

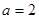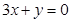∴，方程即.                    ﹍﹍﹍﹍﹍﹍﹍2分

若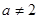，由于截距存在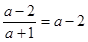，∴ ，         ﹍﹍﹍﹍﹍﹍﹍3分

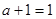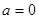即，∴，   方程即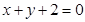.     ﹍﹍﹍﹍﹍﹍﹍﹍5分

(2)法一：将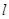的方程化为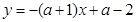，     ﹍﹍﹍﹍﹍﹍﹍﹍7分

∴欲使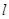不经过第二象限，当且仅当 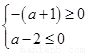   ﹍﹍﹍﹍﹍﹍﹍9分

∴a≤－1.           所以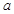的取值范围是a≤－1.     ﹍﹍﹍﹍﹍﹍10分

法二：将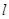的方程化为(x＋y＋2)＋a(x－1)＝0(a∈R)，    ﹍﹍﹍﹍﹍﹍﹍7分

它表示过l₁：x＋y＋2＝0与l₂：x－1＝0的交点(1，－3)的直线系(不包括x＝1)．由图象可知l的斜率－(a＋1)≥0时，l不经过第二象限，∴a≤－1.   ﹍﹍﹍﹍﹍﹍﹍﹍10分

考点：本题主要考查直线方程的一般式，直线在坐标轴上的截距的定义，直线在坐标系中的位置与它的斜率、截距的关系，属于基础题

点评:解决该试题的易错点是对于直线在坐标轴上截距相等的理解中，缺少过原点的情况的分析。