
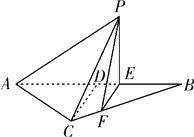
【题目】如图所示,等腰![]() 的底边
的底边![]() ,高
,高![]() ,点
,点![]() 是线段
是线段![]() 上异于点
上异于点![]() 的动点,点
的动点,点![]() 在
在![]() 边上,且
边上,且![]() ,现沿
,现沿![]() 将△
将△![]() 折起到△
折起到△![]() 的位置,使
的位置,使![]() ,记
,记![]() ,
, ![]() 表示四棱锥
表示四棱锥![]() 的体积.
的体积.
(1)求![]() 的表达式;(2)当
的表达式;(2)当![]() 为何值时,
为何值时, ![]() 取得最大,并求最大值。
取得最大,并求最大值。
【答案】(1) VP-ACFE=![]() (2)
(2) ![]()
![]()
【解析】试题分析:(1)![]() ,S四边形ACFE=S△ABC-S△BEF=
,S四边形ACFE=S△ABC-S△BEF=![]() ,所以四棱锥P-ACFE的体积VP-ACFE=
,所以四棱锥P-ACFE的体积VP-ACFE=![]() S四边形ACFE·PE=
S四边形ACFE·PE=![]() ;(2)V′(x)=0
;(2)V′(x)=0 ![]() ,所以
,所以![]()
![]() 。
。
试题解析:
(1)因为EF⊥AB,所以EF⊥PE.又因为PE⊥AE,EF∩AE=E,所以PE⊥平面ACFE. 因为EF⊥AB,CD⊥AB,且CD,EF共面,所以EF∥CD,
所以![]()
![]()
所以四边形ACFE的面积
S四边形ACFE=S△ABC-S△BEF=![]()
所以四棱锥P-ACFE的体积VP-ACFE=![]() S四边形ACFE·PE=
S四边形ACFE·PE=![]()
(2)由(1)知. ![]() 令V′(x)=0
令V′(x)=0 ![]() 因为当
因为当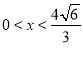 时,V′(x)>0, 当
时,V′(x)>0, 当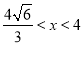 时,V′(x)<0.所以当
时,V′(x)<0.所以当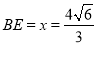 时,
时, 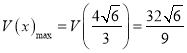


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】一牧羊人赶着一群羊通过4个关口,每过一个关口,守关人将拿走当时羊的一半,然后退还一只给牧羊人,过完这些关口后,牧羊人只剩下3只羊,则牧羊人在过第1个关口前有_________只羊.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,则下列命题中正确的个数是( )
,则下列命题中正确的个数是( )
①当![]() 时,函数
时,函数![]() 在
在![]() 上是单调增函数;
上是单调增函数;
②当![]() 时,函数
时,函数![]() 在
在![]() 上有最小值;
上有最小值;
③函数![]() 的图象关于点
的图象关于点![]() 对称;
对称;
④方程![]() 可能有三个实数根.
可能有三个实数根.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知cos(75°+α)=![]() ,α是第三象限角,
,α是第三象限角,
(1)求sin(75°+α) 的值.
(2)求cos(α-15°) 的值.
(3)求sin(195°-α)+cos(105o-α)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若在定义域内存在
,若在定义域内存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 为函数
为函数![]() 的局部对称点.
的局部对称点.
(1)若![]() ,证明:函数
,证明:函数![]() 必有局部对称点;
必有局部对称点;
(2)若函数![]() 在区间
在区间![]() 内有局部对称点,求实数
内有局部对称点,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 在
在![]() 上有局部对称点,求实数
上有局部对称点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com