
【题目】已知![]() ,
, ![]() 为两条不同的直线,
为两条不同的直线, ![]() ,
, ![]() 为两个不同的平面,对于下列四个命题:
为两个不同的平面,对于下列四个命题:
①![]() ,
, ![]() ,
, ![]() ,
, ![]() ②
②![]() ,
, ![]()
③![]() ,
, ![]() ,
, ![]() ④
④![]() ,
, ![]()
其中正确命题的个数有( )
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(2)如果对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)是否存在实数![]() ,使得函数
,使得函数![]() 的最大值为0,若存在,求出
的最大值为0,若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,an+1= ![]() (n∈N*).
(n∈N*).
(1)求证:{ ![]() +
+ ![]() }是等比数列,并求{an}的通项公式an;
}是等比数列,并求{an}的通项公式an;
(2)数列{bn}满足bn=(3n﹣1) ![]() an , 数列{bn}的前n项和为Tn , 若不等式(﹣1)nλ<Tn+
an , 数列{bn}的前n项和为Tn , 若不等式(﹣1)nλ<Tn+ ![]() 对一切n∈N*恒成立,求λ的取值范围.
对一切n∈N*恒成立,求λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校1800名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组![]() ,第二组
,第二组![]() ,,第五组
,,第五组![]() ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.

(1)若成绩小于15秒认为良好,求该样本在这次百米测试中成绩良好的人数;
(2)请估计学校1800名学生中,成绩属于第四组的人数;
(3)请根据频率分布直方图,求样本数据的众数和中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的首项a1=a(a>0),其前n项和为Sn , 设bn=an+an+1(n∈N*).
(1)若a2=a+1,a3=2a2 , 且数列{bn}是公差为3的等差数列,求S2n;
(2)设数列{bn}的前n项和为Tn , 满足Tn=n2 .
①求数列{an}的通项公式;
②若对n∈N*,且n≥2,不等式(an﹣1)(an+1-1)≥2(1﹣n)恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量.产品数量的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95)由此得到频率分布直方图如图.则产品数量位于[55,65)范围内的频率为;这20名工人中一天生产该产品数量在[55,75)的人数是 . 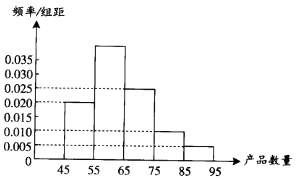
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com