
【题目】(本小题满分12分)
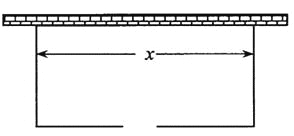
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元)。
(Ⅰ)将y表示为x的函数;
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
【答案】(Ⅰ)y=225x+![]()
(Ⅱ)当x=24m时,修建围墙的总费用最小,最小总费用是10440元。
【解析】
试题(1)设矩形的另一边长为am,则根据围建的矩形场地的面积为360m2,易得![]() ,此时再根据旧墙的维修费用为45元/m,新墙的造价为180元/m,我们即可得到修建围墙的总费用y表示成x的函数的解析式;(2)根据(1)中所得函数的解析式,利用基本不等式,我们易求出修建此矩形场地围墙的总费用最小值,及相应的x值
,此时再根据旧墙的维修费用为45元/m,新墙的造价为180元/m,我们即可得到修建围墙的总费用y表示成x的函数的解析式;(2)根据(1)中所得函数的解析式,利用基本不等式,我们易求出修建此矩形场地围墙的总费用最小值,及相应的x值
试题解析:(1)如图,设矩形的另一边长为a m
则![]() 45x+180(x-2)+180·2a=225x+360a-360
45x+180(x-2)+180·2a=225x+360a-360
由已知xa=360,得a=![]() ,
,
所以y=225x+![]()
(2)![]()
![]() .当且仅当225x=
.当且仅当225x=![]() 时,等号成立.
时,等号成立.
即当x=24m时,修建围墙的总费用最小,最小总费用是10440元.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在xOy平面上,将两个半圆弧(x﹣1)2+y2=1(x≥1)和(x﹣3)2+y2=1(x≥3),两条直线y=1和y=﹣1围成的封闭图形记为D,如图中阴影部分,记D绕y轴旋转一周而成的几何体为Ω.过(0,y)(|y|≤1)作Ω的水平截面,所得截面积为4π ![]() +8π.试利用祖暅原理、一个平放的圆柱和一个长方体,得出Ω的体积值为 .
+8π.试利用祖暅原理、一个平放的圆柱和一个长方体,得出Ω的体积值为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱柱ABC﹣A1B1C1的侧棱与底面垂直,体积为 ![]() ,底面是边长为
,底面是边长为 ![]() 的正三角形,若P为底面A1B1C1的中心,则PA与平面A1B1C1所成角的大小为( )
的正三角形,若P为底面A1B1C1的中心,则PA与平面A1B1C1所成角的大小为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名高三学生平均每天课外体育锻炼时间进行调查,如表:(平均每天锻炼的时间单位:分钟)
平均每天锻炼的时间/分钟 |
|
|
|
|
|
|
总人数 | 20 | 36 | 44 | 50 | 40 | 10 |
将学生日均课外体育锻炼时间在![]() 的学生评价为“课外体育达标”.
的学生评价为“课外体育达标”.
(1)请根据上述表格中的统计数据填写下面的![]() 列联表;
列联表;
课外体育不达标 | 课外体育达标 | 合计 | |
男 | |||
女 | 20 | 110 | |
合计 |
(2)通过计算判断是否能在犯错误的概率不超过![]() 的前提下认为“课外体育达标”性别有关?
的前提下认为“课外体育达标”性别有关?
参考公式![]() ,其中
,其中![]()
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 在线段
在线段![]() 上.过点
上.过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,将
,将![]() 沿
沿![]() 折起到
折起到![]() 的位置(点
的位置(点![]() 与
与![]() 重合),使得
重合),使得![]() .
.

(Ⅰ)求证:![]() .
.
(Ⅱ)试问:当点![]() 在线段
在线段![]() 上移动时,二面角
上移动时,二面角![]() 的平面角的余弦值是否为定值?若是,求出其定值;若不是,说明理由.
的平面角的余弦值是否为定值?若是,求出其定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=aex,g(x)=lnx-lna,其中a为常数,且曲线y=f(x)在其与y轴的交点处的切线记为l1,曲线y=g(x)在其与x轴的交点处的切线记为l2,且l1∥l2.
(1)求l1,l2之间的距离;
(2)若存在x使不等式![]() 成立,求实数m的取值范围;
成立,求实数m的取值范围;
(3)对于函数f(x)和g(x)的公共定义域中的任意实数x0,称|f(x0)-g(x0)|的值为两函数在x0处的偏差.求证:函数f(x)和g(x)在其公共定义域内的所有偏差都大于2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com