
设函数
(1)解不等式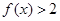 ;
;
(2)求函数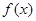 的最小值.
的最小值.
(1)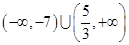 ;(2)
;(2) .
.
解析试题分析:(1)解含绝对值的不等式,关键是去掉绝对值符号,其方法有三种:①定义法;②平方法;③分区间讨论法,这里用的是分区间讨论法,遇到多个绝对值时常用此方法;(2)求绝对值函数的值域,通常是通过分区间讨论,去掉绝对值符号,将绝对值函数改写成分段函数,然后就每段求 的范围,最后再将每段求得的范围求并集,注意不是求交集,从而得到绝对值函数的值域.
的范围,最后再将每段求得的范围求并集,注意不是求交集,从而得到绝对值函数的值域.
试题解析:(1)不等式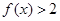 等价于:
等价于:
① ;
;
②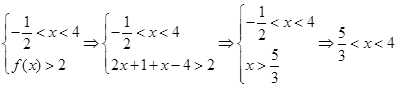 ;
;
③ ,
,
综合①②③得不等式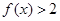 的解集为:
的解集为: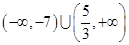 5分
5分
(2)①当 时,
时, ;
;
②当 时,
时,
③当 时,
时,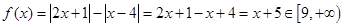
综合①②③得函数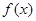 的值域为
的值域为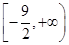 ,因此求函数
,因此求函数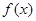 的最小值为
的最小值为 . 10分
. 10分
考点:1.含绝对值的不等式的解法;2.绝对值函数的值域的求法;3.分类讨论思想.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com