若函数f(x)满足:对于任意x1,x2>0,都有f(x1)>0,f(x2)>0且f(x1)+f(x2)<f(x1+x2)成立,则称函数f(x)具有性质M.给出下列四个函数:①y=x3,②y=log2(x+1),③y=2x-1,④y=sinx.其中具有性质M的函数是 (注:把满足题意所有函数的序号都填上)
【答案】
分析:根据题意依次分析命题:①②③通过做差比较f(x
1)+f(x
2)-f(x
1+x
2)大于还是小于零,得出结论;④当x>0时,根据函数y=sinx的值域是[-1,1],得出结论即可.
解答:解:①函数y=x
3,当x>0时,y>0
f(x
1)+f(x
2)-f(x
1+x
2)=x
13+x
23-(x
1+x
2)
3=-3x
12x
2-3x
22x
1<0∴f(x
1)+f(x
2)<f(x
1+x
2) 故①具有性质M的函数;
②当x
1,x
2>0时,y=log
2(x+1)>0
f(x
1)+f(x
2)-f(x
1+x
2)=log
2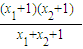
∵x
1,x
2>0
∴f(x
1)+f(x
2)-f(x
1+x
2)=log
2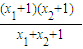
>0
即f(x
1)+f(x
2)>f(x
1+x
2)
故②不具有性质M的函数;
③当x>0时,y=2
x-1的值域(0,+∞)
f(x
1)+f(x
2)-f(x
1+x
2)=2
x1-1+2
x2-1-2
x1+x2+1>0 故③具有性质M的函数;
④当x>0时,函数y=sinx的值域是[-1,1],故不具有M的性质.
可通过作差比较得到结论.
故答案为①③.
点评:本题考查了对数函数、正弦函数、指数函数的单调性以及值域,对于比较两数大小一般采取做差比较的方法.属于基础题.

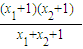
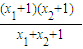 >0
>0

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案