
【题目】已知抛物线![]() 的焦点为F,点P为抛物线C上一点,
的焦点为F,点P为抛物线C上一点,![]() ,O为坐标原点,
,O为坐标原点,![]() .
.
(1)求抛物线C的方程;
(2)设Q为抛物线C的准线上一点,过点F且垂直于OQ的直线交抛物线C于A,B两点记![]() ,
,![]() 的面积分别为
的面积分别为![]()
![]() ,求
,求![]() 的取值范围.
的取值范围.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】“纹样”是中国艺术宝库的瑰宝,“火纹”是常见的一种传统纹样,为了测算某火纹纹样(如图阴影部分所示)的面积,作一个边长为3的正方形将其包含在内,并向该正方形内随机投掷2000个点,己知恰有800个点落在阴影部分,据此可估计阴影部分的面积是

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象上所有点的纵坐标不变,横坐标变为原来的
的图象上所有点的纵坐标不变,横坐标变为原来的![]() ,再将所得图象向右平移
,再将所得图象向右平移![]() 个单位,若得到的图象关于原点对称,则当
个单位,若得到的图象关于原点对称,则当![]() 时,
时,![]() 的值域为( )
的值域为( )
A.![]() B.
B.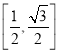 C.
C.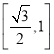 D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 的棱长均为2,O为AC的中点,平面A'OB⊥平面ABC,平面
的棱长均为2,O为AC的中点,平面A'OB⊥平面ABC,平面![]() ⊥平面ABC.
⊥平面ABC.
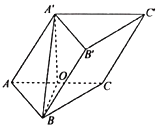
(1)求证:A'O⊥平面ABC;
(2)求二面角A﹣BC﹣C'的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家统计局服务业调查中心和中国物流与采购联合会发布的2018年10月份至2019年9月份共12个月的中国制造业采购经理指数(PMI)如下图所示.则下列结论中错误的是( )
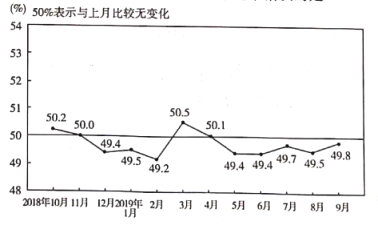
A.12个月的PMI值不低于50%的频率为![]()
B.12个月的PMI值的平均值低于50%
C.12个月的PMI值的众数为49.4%
D.12个月的PMI值的中位数为50.3%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求实数
,求实数![]() ,
,![]() 的值;
的值;
(2)若函数![]() 在
在![]() 和
和![]() 两处取得极值,求实数
两处取得极值,求实数![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com