
【题目】下列说法正确的有_________.
①函数![]() 的一个对称中心为
的一个对称中心为![]() ;
;
②在![]() 中,
中, ![]() 是
是![]() 的中点,则
的中点,则![]() ;
;
③在![]() 中,
中, ![]() 是
是![]() 的充要条件;
的充要条件;
④定义![]() ,已知
,已知![]() ,则
,则![]() 的最大值为
的最大值为![]() .
.
【答案】①②③④
【解析】 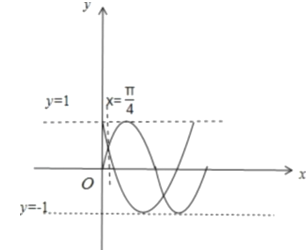
①对于函数![]() ,令
,令![]() ,求得
,求得![]() ,故函数
,故函数![]() 的图象的一个对称中心为
的图象的一个对称中心为![]() ,故①正确;②在
,故①正确;②在![]() 中,
中, ![]() 是
是![]() 的中点,则
的中点,则![]() ,故②正确;③在
,故②正确;③在![]() 中,
中, ![]() ,等价于
,等价于![]() ,等价于
,等价于![]() ,等价于
,等价于![]() ,等价于
,等价于![]() ,等价于
,等价于![]() ,故③正确;④定义
,故③正确;④定义![]() ,已知
,已知![]() ,画出
,画出![]() 和
和![]() 的图象,如图所示,则由图可知,当
的图象,如图所示,则由图可知,当![]() 时,
时, ![]() 取得最大值为
取得最大值为![]() ,故④正确,故答案为①②③④.
,故④正确,故答案为①②③④.
【 方法点睛】本题主要通过对多个命题真假的判断,主要综合考查向量的线性运算及三角函数的图象与性质,属于难题.这种题型综合性较强,也是高考的命题热点,同学们往往因为某一处知识点掌握不好而导致“全盘皆输”,因此做这类题目更要细心、多读题,尽量挖掘出题目中的隐含条件,另外,要注意从简单的自己已经掌握的知识点入手,然后集中精力突破较难的命题.


科目:高中数学 来源: 题型:
【题目】随着人们对环境关注度的提高,绿色低碳出行越来越受到市民重视. 为此贵阳市建立了公共自行车服务系统,市民凭本人二代身份证到自行车服务中心办理诚信借车卡借车,初次办卡时卡内预先赠送20积分,当积分为0时,借车卡将自动锁定,限制借车,用户应持卡到公共自行车服务中心以1元购1个积分的形式再次激活该卡,为了鼓励市民租用公共自行车出行,同时督促市民尽快还车,方便更多的市民使用,公共自行车按每车每次的租用时间进行扣分收费,具体扣分标准如下:
①租用时间不超过1小时,免费;
②租用时间为1小时以上且不超过2小时,扣1分;
③租用时间为2小时以上且不超过3小时,扣2分;
④租用时间超过3小时,按每小时扣2分收费(不足1小时的部分按1小时计算).
甲、乙两人独立出行,各租用公共自行车一次,两人租车时间都不会超过3小时,设甲、乙租用时间不超过1小时的概率分别是0.4和0.5;租用时间为1小时以上且不超过2小时的概率分别是0.4和0.3.
(1)求甲、乙两人所扣积分相同的概率;
(2)设甲、乙两人所扣积分之和为随机变量![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设进入某商场的每一位顾客购买甲种商品的概率为0.5,购买乙种商品的概率为0.6,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的.
(1)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(2)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(3)记ξ表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求ξ的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】实数m取什么数值时,复数z=m2﹣1+(m2﹣m﹣2)i分别是:
(1)实数?
(2)虚数?
(3)纯虚数?
(4)表示复数z的点在复平面的第四象限?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是定义域为R的偶函数,当x≥0时,f(x)= 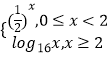 ,若关于x的方程[f(x)]2+af(x)﹣a﹣1=0(a∈R)有且只有7个不同实数根,则a的取值范围是 .
,若关于x的方程[f(x)]2+af(x)﹣a﹣1=0(a∈R)有且只有7个不同实数根,则a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C对边的边长分别是a,b,c,已知c=2,C= ![]() . (Ⅰ)若△ABC的面积等于
. (Ⅰ)若△ABC的面积等于 ![]() ,求a,b;
,求a,b;
(Ⅱ)若sinC+sin(B﹣A)=2sin2A,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com