
| A. | [$\frac{7}{9}$,$\frac{5}{4}$] | B. | [$\frac{5}{9}$,$\frac{3}{4}$] | C. | [$\frac{7}{9}$,$\frac{7}{8}$] | D. | [$\frac{8}{9}$,$\frac{5}{4}$] |
分析 化简可得$\frac{1}{9}$≤1-2f(x)≤$\frac{1}{4}$,令t=$\sqrt{1-2f(x)}$,t∈[$\frac{1}{3}$,$\frac{1}{2}$],从而可得y=$\frac{1-{t}^{2}}{2}$+t=$\frac{-(t-1)^{2}+2}{2}$,从而求值域.
解答 解:∵f(x)的值域为[$\frac{3}{8}$,$\frac{4}{9}$],
∴$\frac{1}{9}$≤1-2f(x)≤$\frac{1}{4}$,
令t=$\sqrt{1-2f(x)}$,t∈[$\frac{1}{3}$,$\frac{1}{2}$],
则f(x)=$\frac{1-{t}^{2}}{2}$,
故y=f(x)+$\sqrt{1-2f(x)}$
=$\frac{1-{t}^{2}}{2}$+t=$\frac{-(t-1)^{2}+2}{2}$,
∵t∈[$\frac{1}{3}$,$\frac{1}{2}$],
∴$\frac{14}{9}$≤-(t-1)2+2≤$\frac{7}{4}$,
∴$\frac{7}{9}$≤$\frac{-(t-1)^{2}+2}{2}$≤$\frac{7}{8}$,
故选:C.
点评 本题考查了函数的值域的求法及换元法的应用.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{18}{25}$ | B. | $-\frac{7}{25}$ | C. | $±\frac{24}{25}$ | D. | $\frac{7}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
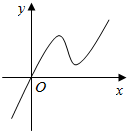 已知函数f(x)的定义域为R,且满足f(4)=1,f′(x)为f(x)的导函数,又知y=f′(x)的图象如图所示,若两个正数a,b满足,f(2a+b)<1,则$\frac{b+2}{a+1}$的取值范围是( )
已知函数f(x)的定义域为R,且满足f(4)=1,f′(x)为f(x)的导函数,又知y=f′(x)的图象如图所示,若两个正数a,b满足,f(2a+b)<1,则$\frac{b+2}{a+1}$的取值范围是( )| A. | $({\frac{2}{3},6})$ | B. | $[{\frac{2}{3},6}]$ | C. | $[\frac{1}{4},\frac{5}{2}]$ | D. | $({\frac{1}{4},\frac{5}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {4} | B. | {3,4} | C. | {2,3,4} | D. | {1,2,3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,$\frac{2}{3}$] | B. | (-1,$\frac{2}{3}$) | C. | (-∞,-1)∪(-1,$\frac{2}{3}$] | D. | [$\frac{2}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 193 | B. | 192 | C. | 191 | D. | 190 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com