
【题目】 依法纳税是每个公民应尽的义务,个人取得的所得应依照《中华人民共和国个人所得税法》向国家缴纳个人所得税(简称个税).![]() 年
年![]() 月
月![]() 日起,个税税额根据应纳税所得额、税率和速算扣除数确定,计算公式为:个税税额=应纳税所得额×税率-速算扣除数.①应纳税所得额的计算公式为:应纳税所得额=综合所得收入额-基本减除费用-专项扣除-专项附加扣除-依法确定的其他扣除.②其中,“基本减除费用”(免征额)为每年
日起,个税税额根据应纳税所得额、税率和速算扣除数确定,计算公式为:个税税额=应纳税所得额×税率-速算扣除数.①应纳税所得额的计算公式为:应纳税所得额=综合所得收入额-基本减除费用-专项扣除-专项附加扣除-依法确定的其他扣除.②其中,“基本减除费用”(免征额)为每年![]() 元.税率与速算扣除数见下表.
元.税率与速算扣除数见下表.
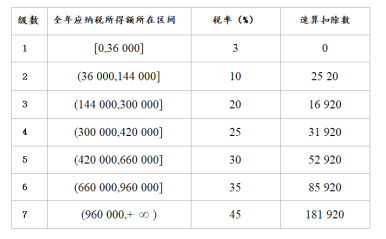
(1)设全年应纳税所得额为![]() ,应缴纳个税税额为
,应缴纳个税税额为![]() ,求
,求![]() 的解析式;
的解析式;
(2)小李全年综合所得收入额为![]() 元,假定缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是
元,假定缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是![]() ,
,![]() ,
,![]() ,
,![]() ,专项附加扣除是
,专项附加扣除是![]() 元,依法确定其他扣除是
元,依法确定其他扣除是![]() 元,那么他全年应缴纳多少综合所得个税?
元,那么他全年应缴纳多少综合所得个税?
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】某教育培训中心共有25名教师,他们全部在校外住宿.为完全起见,学校派专车接送教师们上下班.这个接送任务承包给了司机王师傅,正常情况下王师傅用34座的大客车接送教师.由于每次乘车人数不尽相同,为了解教师们的乘车情况,王师傅连续记录了100次的乘车人数,统计结果如下:
乘车人数 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
频数 | 2 | 4 | 4 | 10 | 16 | 20 | 16 | 12 | 8 | 6 | 2 |
以这100次记录的各乘车人数的频率作为各乘车人数的概率.
(Ⅰ)若随机抽查两次教师们的乘车情况,求这两次中至少有一次乘车人数超过18的概率;
(Ⅱ)有一次,王师傅的大客车出现了故障,于是王师傅准备租一辆小客车来临时送一次需要乘车的教师.可供选择的小客车只有20座的![]() 型车和22座的
型车和22座的![]() 型车两种,
型车两种, ![]() 型车一次租金为80元,
型车一次租金为80元, ![]() 型车一次租金为90元.若本次乘车教师的人数超过了所租小客车的座位数,王师傅还要付给多出的人每人20元钱供他们乘出租车.以王师傅本次付出的总费用的期望值为依据,判断王师傅租哪种车较合算?
型车一次租金为90元.若本次乘车教师的人数超过了所租小客车的座位数,王师傅还要付给多出的人每人20元钱供他们乘出租车.以王师傅本次付出的总费用的期望值为依据,判断王师傅租哪种车较合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.
(1)当0≤x≤200时,求函数v(x)的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=xv(x)可以达到最大,并求出最大值.(精确到1辆/小时).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,椭圆上的点到左焦点
,椭圆上的点到左焦点![]() 的距离的最大值为
的距离的最大值为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点.在
两点.在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 且
且![]() ,若存在,求出实数
,若存在,求出实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 是
是![]() 的中点,点
的中点,点![]() 沿着路径
沿着路径![]() 在正方形边上运动所经过的路程为
在正方形边上运动所经过的路程为![]() ,
,![]() 的面积为
的面积为![]() .
.

(1)求![]() 的解析式及定义域;
的解析式及定义域;
(2)求![]() 面积的最大值及此时点
面积的最大值及此时点![]() 位置.
位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:![]() ,点
,点![]() 在x轴的正半轴上,过点M的直线l与抛线C相交于A、B两点,O为坐标原点.
在x轴的正半轴上,过点M的直线l与抛线C相交于A、B两点,O为坐标原点.
![]() 若
若![]() ,且直线l的斜率为1,求证:以AB为直径的圆与抛物线C的准线相切;
,且直线l的斜率为1,求证:以AB为直径的圆与抛物线C的准线相切;
![]() 是否存在定点M,使得不论直线l绕点M如何转动,
是否存在定点M,使得不论直线l绕点M如何转动,![]() 恒为定值?若存在,请求出点M的坐标;若不存在,请说明理由.
恒为定值?若存在,请求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
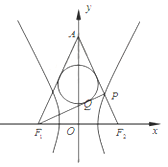
【题目】如图,已知双曲线![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,
,![]() 是双曲线右支上的一点,
是双曲线右支上的一点,![]() 与
与![]() 轴交于点
轴交于点![]() 的内切圆在边
的内切圆在边![]() 上的切点为
上的切点为![]() ,若
,若![]() ,则双曲线的离心率是 ( )
,则双曲线的离心率是 ( )
A. 2 B. ![]() C.
C. ![]() D. 3
D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种化工产品,该产品若以每吨10万元的价格销售,每年可售出1000吨,若将该产品每吨分价格上涨![]() ,则每年的销售数量将减少
,则每年的销售数量将减少![]() ,其中m为正常数,销售的总金额为y万元.
,其中m为正常数,销售的总金额为y万元.
(1)当![]() 时,该产品每吨的价格上涨百分之几,可使销售总金额最大?
时,该产品每吨的价格上涨百分之几,可使销售总金额最大?
(2)当![]() 时,若能使销售总金额比涨价前增加,试设定m的取值范围.
时,若能使销售总金额比涨价前增加,试设定m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com