
 A55=60(种).
A55=60(种).

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:湖南省浏阳一中2010-2011学年高二第一次阶段性考试数学理科试题 题型:044
(1)3人坐在有八个座位的一排上,若每人的左右两边都要有空位,则不同坐法的种数为几种?
(2)有5个人并排站成一排,如果甲必须在乙的右边,则不同的排法有多少种?
(3)现有10个保送上大学的名额,分配给7所学校,每校至少有1个名额,问名额分配的方法共有多少种?
查看答案和解析>>
科目:高中数学 来源:2010-2011年辽宁省高二下学期第二次考试理数 题型:解答题
.(12分)
(1)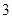 人坐在有八个座位的一排上,若每人的左右两边都要有空位,则不同的坐法的种数为几种?
人坐在有八个座位的一排上,若每人的左右两边都要有空位,则不同的坐法的种数为几种?
(2)甲、乙、丙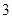 人站在共有
人站在共有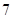 级的台阶上,若每级台阶最多站
级的台阶上,若每级台阶最多站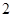 人,同一级台阶上
人,同一级台阶上
不区分站的位置,则有多少种不同的站法?
(3)现有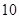 个保送大学的名额,分配给
个保送大学的名额,分配给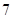 所学校,每校至少
所学校,每校至少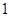 个名额,问名额分配的方法共有多少种?
个名额,问名额分配的方法共有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com