
(1)求证:fn(x)≥nx.
(2)是否存在区间[a,0](a<0),使函数n(x)=f3(x)-f2(x)在区间[a,0]上的值域为[ka,0]?若存在,求出最小的k值及相应的区间[a,0];若不存在,说明理由.
解:(1)证明:fn(x)-nx=(1+x)n-1-nx,
令g(x)=(1+x)n-1-nx,则g′(x)=n[(1+x)n-1-1],
当x∈(-2,0)时,g′(x)<0;
当x∈(0,+∞)时,g′x>0.
∴g(x)在x=0处取得极小值g(0)=0,同时g(x)是学峰函数,则g(0)也是最小值,∴g(x)≥0.
即fn(x)≥nx(当且仅当x=0取等号).
(2)h(x)=f3(x)=f2(x)=x(1+x)2,
h′(x)=(1+x)2+x·2(1+x)=(1+x)(1+3x),
令h′(x)=0,得x=-1,x=-![]() ∴当x∈(-2,-1)时,h′(x)>0;当x∈(-1,-
∴当x∈(-2,-1)时,h′(x)>0;当x∈(-1,-![]() )时,h′(x)<0;
)时,h′(x)<0;
当x∈(-![]() ,+∞)时,h′(x)>0,故h(x)的草图如图所示:
,+∞)时,h′(x)>0,故h(x)的草图如图所示:
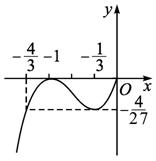
①在-![]() ≤a<0时,h(x)最小值h(a)=ka.∴k=(1+a)2≥
≤a<0时,h(x)最小值h(a)=ka.∴k=(1+a)2≥![]() ,
,
②在-![]() ≤a≤-
≤a≤-![]() 时,h(x)最小值=h(-
时,h(x)最小值=h(-![]() )=-
)=-![]() =ka,k=-
=ka,k=-![]() ,
,![]() ≤k≤
≤k≤![]() ;
;
③在a≤-![]() 时,h(x)最小值=h(a)=a(1+a)2=ka,k=(1+a)2≥
时,h(x)最小值=h(a)=a(1+a)2=ka,k=(1+a)2≥![]() ,a=-
,a=-![]() 取等号.
取等号.
综上k的最小值为![]() ,此时[a,0]=[-
,此时[a,0]=[-![]() ,0].
,0].


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| f | ′ n |
| ||
|
| fn(1) |
| fn+1(1) |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求证fn(x)≥nx;
(2)设![]() ,求证0<x0<1;
,求证0<x0<1;
(3)是否存在区间[a,b)![]() (-∞,0],使函数h(x)=f3(x)-f2(x)在区间[a,b)的值域为[ka,kb]?若存在,求出最小的A的值及相应的区间[a,b].
(-∞,0],使函数h(x)=f3(x)-f2(x)在区间[a,b)的值域为[ka,kb]?若存在,求出最小的A的值及相应的区间[a,b].
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com