
【题目】甲、乙、丙三人进行羽毛球练习赛,其中两人比赛,另一人当裁判,每局比赛结束时,负的一方在下一局当裁判,设各局中双方获胜的概率均为 ![]() ,各局比赛的结果都相互独立,第1局甲当裁判.
,各局比赛的结果都相互独立,第1局甲当裁判.
(1)求第4局甲当裁判的概率;
(2)X表示前4局中乙当裁判的次数,求X的数学期望.
【答案】
(1)解:令A1表示第2局结果为甲获胜.A2表示第3局甲参加比赛时,结果为甲负.A表示第4局甲当裁判.
则A=A1A2,P(A)=P(A1A2)=P(A1)P(A2)= ![]() ;
;
(2)解:X的所有可能值为0,1,2.令A3表示第3局乙和丙比赛时,结果为乙胜.
B1表示第1局结果为乙获胜,B2表示第2局乙和甲比赛时,结果为乙胜,B3表示第3局乙参加比赛时,结果为乙负,
则P(X=0)=P(B1B2 ![]() )=P(B1)P(B2)P(
)=P(B1)P(B2)P( ![]() )=
)= ![]() .
.
P(X=2)=P( ![]() B3)=P(
B3)=P( ![]() )P(B3)=
)P(B3)= ![]() .
.
P(X=1)=1﹣P(X=0)﹣P(X=2)= ![]() .
.
从而EX=0× ![]() +1×
+1× ![]() +2×
+2× ![]() =
= ![]() .
.
【解析】(1)令A1表示第2局结果为甲获胜,A2表示第3局甲参加比赛时,结果为甲负,A表示第4局甲当裁判,分析其可能情况,每局比赛的结果相互独立且互斥,利用独立事件、互斥事件的概率求解即可.(2)X的所有可能值为0,1,2.分别求出X取每一个值的概率,列出分布列后求出期望值即可.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】如图,已知正四棱锥P﹣ABCD中,PA=AB=2,点M,N分别在PA,BD上,且 ![]() =
= ![]() .
. 
(1)求异面直线MN与PC所成角的大小;
(2)求二面角N﹣PC﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率
的离心率![]() ,过椭圆的上顶点
,过椭圆的上顶点![]() 和右顶点
和右顶点![]() 的直线与原点
的直线与原点![]() 的距离为
的距离为![]() ,
,
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在直线![]() 经过椭圆左焦点与椭圆
经过椭圆左焦点与椭圆![]() 交于
交于![]() ,
,![]() 两点,使得以线段
两点,使得以线段![]() 为直径的圆恰好经过坐标原点
为直径的圆恰好经过坐标原点![]() ?若存在,求出直线
?若存在,求出直线![]() 方程;若不存在,请说明理由.
方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱柱ABCD﹣A1B1C1D1的底面是边长为2的菱形,且∠BAD= ![]() ,AA1⊥平面ABCD,AA1=1,设E为CD中点
,AA1⊥平面ABCD,AA1=1,设E为CD中点 
(1)求证:D1E⊥平面BEC1
(2)点F在线段A1B1上,且AF∥平面BEC1 , 求平面ADF和平面BEC1所成锐角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校1800名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50名学生组成一个样本,将测试结果按如下方式分成五组:第一组![]() ,第二组
,第二组![]() ……,第五组
……,第五组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.
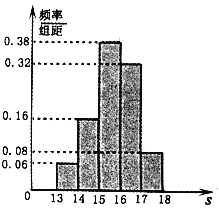
(1)请估计学校1800名学生中,成绩属于第四组的人数;
(2)若成绩小于15秒认为良好,求该样本中在这次百米测试中成绩良好的人数;
(3)请根据频率分布直方图,求样本数据的众数、平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:①第二象限角比第一象限角大;②设![]() 是第二象限角,则
是第二象限角,则![]() ;③三角形的内角是第一象限角或第二象限角;④函数
;③三角形的内角是第一象限角或第二象限角;④函数![]() 是最小正周期为
是最小正周期为![]() 的周期函数;⑤在△ABC中,若
的周期函数;⑤在△ABC中,若![]() ,则A>B.其中正确的是___________ (写出所有正确说法的序号)
,则A>B.其中正确的是___________ (写出所有正确说法的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线的中心在原点,对称轴为坐标轴,一条渐近线方程为![]() ,右焦点
,右焦点![]() ,双曲线的实轴为
,双曲线的实轴为![]() ,
,![]() 为双曲线上一点(不同于
为双曲线上一点(不同于![]() ,
,![]() ),直线
),直线![]() ,
,![]() 分别与直线
分别与直线![]() 交于
交于![]() ,
,![]() 两点.
两点.
(![]() )求双曲线的方程.
)求双曲线的方程.
(![]() )证明
)证明![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com