


 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
在人寿保险业中,要重视某一年龄的投保人的死亡率,经过随机抽样统计,得到某城市一个投保人能活到75岁的概率为0.60,试问:
(1)3个投保人都能活到75岁的概率;
(2)3个投保人中只有1人能活到75岁的概率;
(3)3个投保人中至少有1人能活到75岁的概率.(结果精确到0.01)
查看答案和解析>>
科目:高中数学 来源:2014届山西省高二下学期期中考试理科数学试卷(解析版) 题型:解答题
在人寿保险业中,要重视某一年龄的投保人的死亡率,经过随机抽样统计,得到某市一个投保人能活到75岁的概率为0.60,试问:
(1)若有3个投保人, 求能活到75岁的投保人数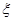 的分布列;
的分布列;
(2)3个投保人中至少有1人能活到75岁的概率.(结果精确到0.01)
查看答案和解析>>
科目:高中数学 来源:湖南模拟 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com