
【题目】已知椭圆C: ![]() 的左右焦点与其短轴的一个端点是正三角形的三个顶点,点D
的左右焦点与其短轴的一个端点是正三角形的三个顶点,点D ![]() 在椭圆C上,直线l:y=kx+m与椭圆C相交于A、P两点,与x轴、y轴分别相交于点N和M,且PM=MN,点Q是点P关于x轴的对称点,QM的延长线交椭圆于点B,过点A、B分别作x轴的垂涎,垂足分别为A1、B1
在椭圆C上,直线l:y=kx+m与椭圆C相交于A、P两点,与x轴、y轴分别相交于点N和M,且PM=MN,点Q是点P关于x轴的对称点,QM的延长线交椭圆于点B,过点A、B分别作x轴的垂涎,垂足分别为A1、B1
(1)求椭圆C的方程;
(2)是否存在直线l,使得点N平分线段A1B1?若存在,求求出直线l的方程,若不存在,请说明理由.
【答案】
(1)
解:∵椭圆C: ![]() 的左右焦点与其短轴的一个端点是正三角形的三个顶点,点D
的左右焦点与其短轴的一个端点是正三角形的三个顶点,点D ![]() 在椭圆C上,
在椭圆C上,
∴由题意得 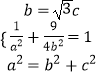 ,解得a2=4,b2=3,
,解得a2=4,b2=3,
∴椭圆C的方程为 ![]()
(2)
解:假设存在这样的直线l:y=kx+m,∴M(0,m),N(﹣ ![]() ,0),
,0),
∵PM=MN,∴P( ![]() ,2m),Q(
,2m),Q( ![]() ),
),
∴直线QM的方程为y=﹣3kx+m,
设A(x1,y1),由 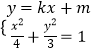 ,得(3+4k2)x2+8kmx+4(m2﹣3)=0,
,得(3+4k2)x2+8kmx+4(m2﹣3)=0,
∴ ![]() ,∴
,∴ ![]() ,
,
设B(x2,y2),由  ,得(3+36k2)x2﹣24kmx+4(m2﹣3)=0,
,得(3+36k2)x2﹣24kmx+4(m2﹣3)=0,
∴x2+ ![]() =
= ![]() ,∴x2=﹣
,∴x2=﹣ ![]() ,
,
∵点N平分线段A1B1,∴ ![]() ,
,
∴﹣ ![]() =﹣
=﹣ ![]() ,∴k=
,∴k= ![]() ,
,
∴P(±2m,2m),∴ ![]() ,解得m=
,解得m= ![]() ,
,
∵|m|= ![]() <b=
<b= ![]() ,∴△>0,符合题意,
,∴△>0,符合题意,
∴直线l的方程为y= ![]()
【解析】(1)由椭圆的左右焦点与其短轴的一个端点是正三角形的三个顶点,点D ![]() 在椭圆C上,列出方程组,求出a,b,由此能求出椭圆C的方程.(2)假设存在这样的直线l:y=kx+m,则直线QM的方程为y=﹣3kx+m,由
在椭圆C上,列出方程组,求出a,b,由此能求出椭圆C的方程.(2)假设存在这样的直线l:y=kx+m,则直线QM的方程为y=﹣3kx+m,由 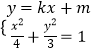 ,得(3+4k2)x2+8kmx+4(m2﹣3)=0,由
,得(3+4k2)x2+8kmx+4(m2﹣3)=0,由  ,得(3+36k2)x2﹣24kmx+4(m2﹣3)=0,由此利用根的判别式、韦达定理、中点坐标公式,结合已知条件,能求出直线l的方程.
,得(3+36k2)x2﹣24kmx+4(m2﹣3)=0,由此利用根的判别式、韦达定理、中点坐标公式,结合已知条件,能求出直线l的方程.
【考点精析】关于本题考查的椭圆的标准方程,需要了解椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能得出正确答案.
才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinωx﹣ ![]() cosωx(ω>0),若方程f(x)=﹣1在(0,π)上有且只有四个实数根,则实数ω的取值范围为( )
cosωx(ω>0),若方程f(x)=﹣1在(0,π)上有且只有四个实数根,则实数ω的取值范围为( )
A.( ![]() ,
, ![]() ]
]
B.( ![]() ,
, ![]() ]
]
C.( ![]() ,
, ![]() ]
]
D.( ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某知名品牌汽车深受消费者喜爱,但价格昂贵.某汽车经销商推出A、B、C三种分期付款方式销售该品牌汽车,并对近期100位采用上述分期付款的客户进行统计分析,得到如下的柱状图.已知从A、B、C三种分期付款销售中,该经销商每销售此品牌汽车1俩所获得的利润分别是1万元,2万元,3万元.现甲乙两人从该汽车经销商处,采用上述分期付款方式各购买此品牌汽车一辆.以这100位客户所采用的分期付款方式的频率代替1位客户采用相应分期付款方式的概率.
(1)求甲乙两人采用不同分期付款方式的概率;
(2)记X(单位:万元)为该汽车经销商从甲乙两人购车中所获得的利润,求X的分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015![]() 全国统考II)设函数f(x)=ln(1+|x|)-
全国统考II)设函数f(x)=ln(1+|x|)-![]() ,则使得f(x)
,则使得f(x)![]() f(2x-1)成立的x的取值范围是()
f(2x-1)成立的x的取值范围是()
A.(![]() ,1)
,1)
B.(-![]() ,
,![]() )
)![]() (1,+
(1,+![]() )
)
C.(-![]() ,
,![]() )
)
D.(-![]() ,-
,-![]() )
)![]() (
(![]() ,+
,+![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 在直角坐标系xOy中,曲线C1:
在直角坐标系xOy中,曲线C1:![]() (t为参数,且t≠0),其中0
(t为参数,且t≠0),其中0![]()
![]()
![]() , 在以O为极点x轴正半轴为极轴的极坐标系中,曲线C2::
, 在以O为极点x轴正半轴为极轴的极坐标系中,曲线C2::![]() =2sin
=2sin![]() , C3:
, C3:![]() =2
=2![]() cos
cos![]()
(1)求C2与C3交点的直角坐标
(2)若C1与C2相交于点A,C1与C3相交于点B,求|AB|最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
A.16
B.18
C.25
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com