
分析 (1)根据指数幂的运算性质计算即可,
(2)根据对数的运算性质计算即可,
(3)根据函数的定义域的求法得到由$\left\{{\begin{array}{l}{4x-5>0}\\{1-{{log}_2}(4x-5)≥0}\end{array}}\right.$解得即可.
解答 解:(1)${({\sqrt{1000}})^{-\frac{2}{3}}}×{({\root{3}{{{{10}^2}}}})^{\frac{9}{2}}}$=${({{{10}^{\frac{3}{2}}}})^{-\frac{2}{3}}}×{({{{10}^{\frac{2}{3}}}})^{\frac{9}{2}}}$=10-1×103=102=100,
(2)lg20+log10025=$lg20+{log_{{{10}^2}}}{5^2}$=lg20+log105=lg100=2,
(3)由$\left\{{\begin{array}{l}{4x-5>0}\\{1-{{log}_2}(4x-5)≥0}\end{array}}\right.$$⇒\left\{{\begin{array}{l}{x>\frac{5}{4}}\\{x≤\frac{7}{4}}\end{array}⇒\frac{5}{4}<x≤\frac{7}{4}}\right.$
所以f(x)的定义域为$\{x|\frac{5}{4}<x≤\frac{7}{4}\}$
点评 本题考查了指数幂和对数的运算性质以及函数的定义的求法,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=-x2+2x+3,x∈[-1,2)
已知函数f(x)=-x2+2x+3,x∈[-1,2)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
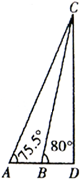 2016年春节期间,小明和小张去上海旅游,参观了东方明珠塔,两人为了测量它的高度,站在A处测得塔尖C的仰角为75.5°,前进38.5m后到达B处,没得塔尖C的仰角为80°,如图所示(其中D为塔底),则东方明珠塔的高度约为( )(参考数据:sin80°≈0.985,sin75.5°≈0.968,sin4.5°≈0.078)
2016年春节期间,小明和小张去上海旅游,参观了东方明珠塔,两人为了测量它的高度,站在A处测得塔尖C的仰角为75.5°,前进38.5m后到达B处,没得塔尖C的仰角为80°,如图所示(其中D为塔底),则东方明珠塔的高度约为( )(参考数据:sin80°≈0.985,sin75.5°≈0.968,sin4.5°≈0.078)| A. | 456m | B. | 438m | C. | 350m | D. | 471m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com