练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知两条直线l1：2x+y﹣2=0与l2：2x﹣my+4=0．
    （1）若直线l1⊥l2 ， 求直线l1与l2交点P的坐标；
    （2）若l1 ， l2以及x轴围成三角形的面积为1，求实数m的值．

    【答案】
    （1）解：∵直线l1⊥l2，∴4﹣m=0，∴m=4，

    联立两条直线l1：2x+y﹣2=0与l2：2x﹣4y+4=0可得P（0.4，1.2）


    （2）解：直线l1：2x+y﹣2=0与x轴的交点坐标为（1，0），l2：2x﹣my+4=0与x轴的交点坐标为（﹣2，0），

    ∵l1，l2以及x轴围成三角形的面积为1，

    ∴三角形的高为 ，

    代入直线l1：2x+y﹣2=0可得x= ，

    （ ， ）代入l2：2x﹣my+4=0可得m=8


    【解析】（1）若直线l1⊥l2，求出m，联立两条直线l1：2x+y﹣2=0与l2：2x﹣4y+4=0求直线l1与l2交点P的坐标；（2）若l1，l2以及x轴围成三角形的面积为1，求出三角形的高，即可求实数m的值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在棱长为1的正方体中，P是侧棱CC1上的一点，CP=m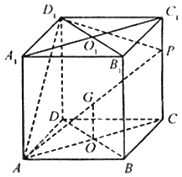
    （1）试确定m，使直线AP与平面BDD1B1所成角的正切值为 ；
    （2）在线段A1C1上是否存在一个定点Q，使得对任意的m，D1Q在平面APD1上的射影垂直于AP，并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知半径为 的圆C，其圆心在射线y=﹣2x（x＜0）上，且与直线x+y+1=0相切．
    （1）求圆C的方程；
    （2）从圆C外一点P（x0 ， y0））向圆引切线PM，M为切点，O为坐标原点，且有|PM|=|PO|，求△PMC面积的最小值，并求此时点P的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，角A，B，C的对边分别是a，b，c，若（2a﹣c）cosB=bcosC．
    （1）求角B的大小，
    （2）若a=3，△ABC的面积为 ，求 的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 ， （Ⅰ）求函数f（x）的单调区间，并判断是否有极值；
    （Ⅱ）若对任意的x＞1，恒有ln（x﹣1）+k+1≤kx成立，求k的取值范围；
    （Ⅲ）证明： （n∈N+ ， n≥2）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数 的值域为 ． （其中[x]表示不大于x的最大整数，例如[3.15]=3，[0.7]=0．）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在雅安发生地震灾害之后，救灾指挥部决定建造一批简易房，供灾区群众临时居住，房形为长方体，高2.5米，前后墙用2.5米高的彩色钢板，两侧用2.5米高的复合钢板，两种钢板的价格都用长度来计算（即钢板的高均为2.5米，用长度乘以单价就是这块钢板的价格），每米单价：彩色钢板为450元，复合钢板为200元，房顶用其他材料建造，每平方米材料费为200元，每套房材料费控制在32000元以内．
    （1）设房前面墙的长为x，两侧墙的长为y，一套简易房所用材料费为p，试用x，y表示p；
    （2）一套简易房面积S的最大值是多少？当S最大时，前面墙的长度是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设l，m是两条不同的直线，α是一个平面，则下列命题正确的是（ ）
    A.若l⊥m，mα，则l⊥α
    B.若l⊥α，l∥m，则m⊥α
    C.若l∥α，mα，则l∥m
    D.若l∥α，m∥α，则l∥m

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，a，b，c分别为角A，B，C的对边，若 ．
    （1）求角A的大小；
    （2）已知 ，求△ABC面积的最大值．

    查看答案和解析>>

    同步练习册答案